内心证等角

乌贼

借鉴forum.php?mod=viewthread&tid=10310&extra=page=1
2楼证明方法
如图：
    $ AI $交圆于$ F $，$ P $为$ BC $与$ FD $交点。有\[ \angle AMP=\angle ABF=\angle ADP \]所以$ AMDP $四点共圆，有\[ \angle BPD=\angle MAD=\angle FBD\riff \triangle FBD\sim \triangle FPB\riff BF^2=FD\cdot FP \]又\[ BF=FI \]因此\[ FI^2=FD\cdot FP\riff\triangle FID\sim \triangle FPI\riff \angle FID=\angle IPF\riff\angle IDA=\angle IPN \]就有$ NEPD $四点共圆，即$ E $为$ \triangle IPD $垂心，所以有\[ \angle KNE=\angle KDP=\angle AMP\riff KN\px AM\riff\angle NIE=\angle NKE=\angle IAE \]

kuing

我的证法后面用到了面积公式和余弦定理，或许可以简化。

证明：要证 `\angle IAD=\angle EID`，只需证 `DI^2=DE\cdot DA`。

作如下图所示的辅助线：

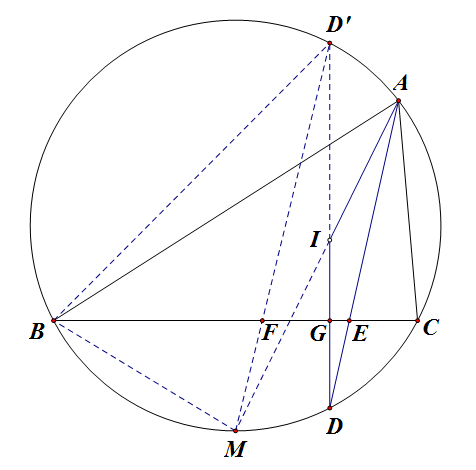
易证 `MI=MB` 且 `\triangle MBF\sim\triangle MD'B`，所以有
\[MI^2=MB^2=MF\cdot MD',\]
而显然 `\triangle IDA\sim\triangle IMD'`，于是要证 `DI^2=DE\cdot DA` 就只需证 `AE:ED=D'F:FM` 即可。

再作垂线 `AH` 及 `MN` 如下图所示：

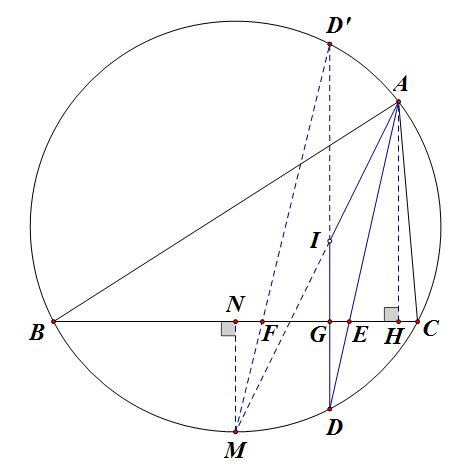
那么
\begin{align*}
\frac{AE}{ED}=\frac{D'F}{FM}&\iff\frac{AH}{DG}=\frac{D'G}{MN}\\
&\iff AH\cdot MN=DG\cdot D'G\\
&\iff AH\cdot MN=BG\cdot CG,\quad(*)
\end{align*}
式 (*) 右边比较简单，因为 `G` 是内切圆与边的切点，所以
\[BG\cdot CG=\frac{a+c-b}2\cdot\frac{a+b-c}2=\frac{a^2-(b-c)^2}4,\]
至于式 (*) 左边，由面积公式易知
\begin{align*}
AH&=\frac{2S}a,\\
MN&=R-R\cos A=\frac{abc}{4S}(1-\cos A),
\end{align*}
那么
\begin{align*}
AH\cdot MN&=\frac12bc(1-\cos A)\\
&=\frac12bc-\frac14(b^2+c^2-a^2)\\
&=\frac{a^2-(b-c)^2}4,
\end{align*}
所以式 (*) 成立，即得证。

乌贼

记一些结论：
   在$ \triangle ABC $中，$ D $在$ BC $上且$ \angle BAD=\angle BCA $，则$ AB $与$ \triangle ADC $的外接圆相切。若将它称为‘圆切现象’，那么这一‘现象’可通过垂心漂移，而且在某些条件下与内心关联……
如图：
   在$ \triangle ABC $中，$ D $在$ BC $上且$ \angle BAD=\angle BCA $，$ E $为$ \triangle ACD $的垂心，$ F $为$ BA $与$ DE $交点，则有\[ \angle AFD=\angle DAE \]