球面勾股定理

hbghlyj

Сферическая теорема Пифагора(奇怪的是, 该词条没有英文版)

直角球面三角形斜边的余弦等于直角边的余弦乘积。\[\cos c=\cos a\cos b\]
我们将使用三面角 $OA_1 B_1 C_1$ 进行证明，平面角 $A_1 OC_1$ 和 $C_1 OB_1$ 等于这个三角形的边 $b$ 和 $a$，平面角 $A_1 OB_1$ 等于它的斜边 $c$，面 $A_1 OC_1$ 和 $C_1 OB_1$ 之间的二面角是直角，其余两个二面角等于球面直角三角形的对应角。该三面角与垂直于射线 $OB_1$ 的平面 $A_1 B_1 C_1$ 相交。那么角 $A_1 C_1 O$ 和 $A_1 C_1 B_1$ 是直角。

由
\begin{align*}
\frac {OB_{1}}{OA_{1}}&=\cos \angle A_{1}OB_{1}=\cos c,\\
\frac {OC_{1}}{OA_{1}}&=\cos \angle A_{1}OC_{1}=\cos b,\\
\frac {OB_{1}}{OC_{1}}&=\cos \angle C_{1}OB_{1}=\cos a.
\end{align*}得\[\cos c={\frac {OB_{1}}{OA_{1}}}={\frac {OB_{1}}{OC_{1}}}\cdot {\frac {OC_{1} }{OA_{1}}}=\cos a\cos b.\]

hbghlyj

三面角余弦定理（en）
球面余弦定理（en | ru）
Let $\mathbf u,\mathbf v$, and $\mathbf w$ denote the unit vectors from the center of the sphere to those corners of the triangle.  The angles and distances do not change if the coordinate system is rotated, so we can rotate the coordinate system so that $\mathbf{u}$ is at the north pole and $\mathbf{v}$ is somewhere on the prime meridian (longitude of 0).  With this rotation, the spherical coordinates for $\mathbf{v}$ are $(r, \theta, \phi) = (1, a, 0)$, where $θ$ is the angle measured from the north pole not from the equator, and the spherical coordinates for $\mathbf{w}$ are $(r, \theta, \phi) = (1, b, C)$.  The Cartesian coordinates for $\mathbf{v}$ are $(x, y, z) = (\sin a, 0, \cos a)$ and the Cartesian coordinates for $\mathbf{w}$ are $(x, y, z) = (\sin b \cos C, \sin b \sin C, \cos b)$.  The value of $\cos c$ is the dot product of the two Cartesian vectors, which is $\sin a \sin b \cos C + \cos a \cos b$.

---

五元公式（ru）
由莱昂哈德·欧拉在18世纪推导出来。三角形的不同角度和边的五个元素的基本公式可以分为两组：

• 有关三边和两个角的公式，也称为边的正弦和角的余弦的公式。\[\sin a\cos B=\cos b\sin c-\sin b\cos c\cos A,\]
• 与三个角和两个边相关的公式，也称为角的正弦与边的余弦的公式。其中一个是：\[\sin A\cos b=\sin C\cos B+\cos C\sin B\cos a,\]
  

使用投影的证明

在边的正弦乘角的余弦公式中，边和与它相邻的角用另外两条边和它们之间的夹角来表示。对于每条边，可以取相邻的两个角中的一个，所以这样的公式总共有六个。
证明
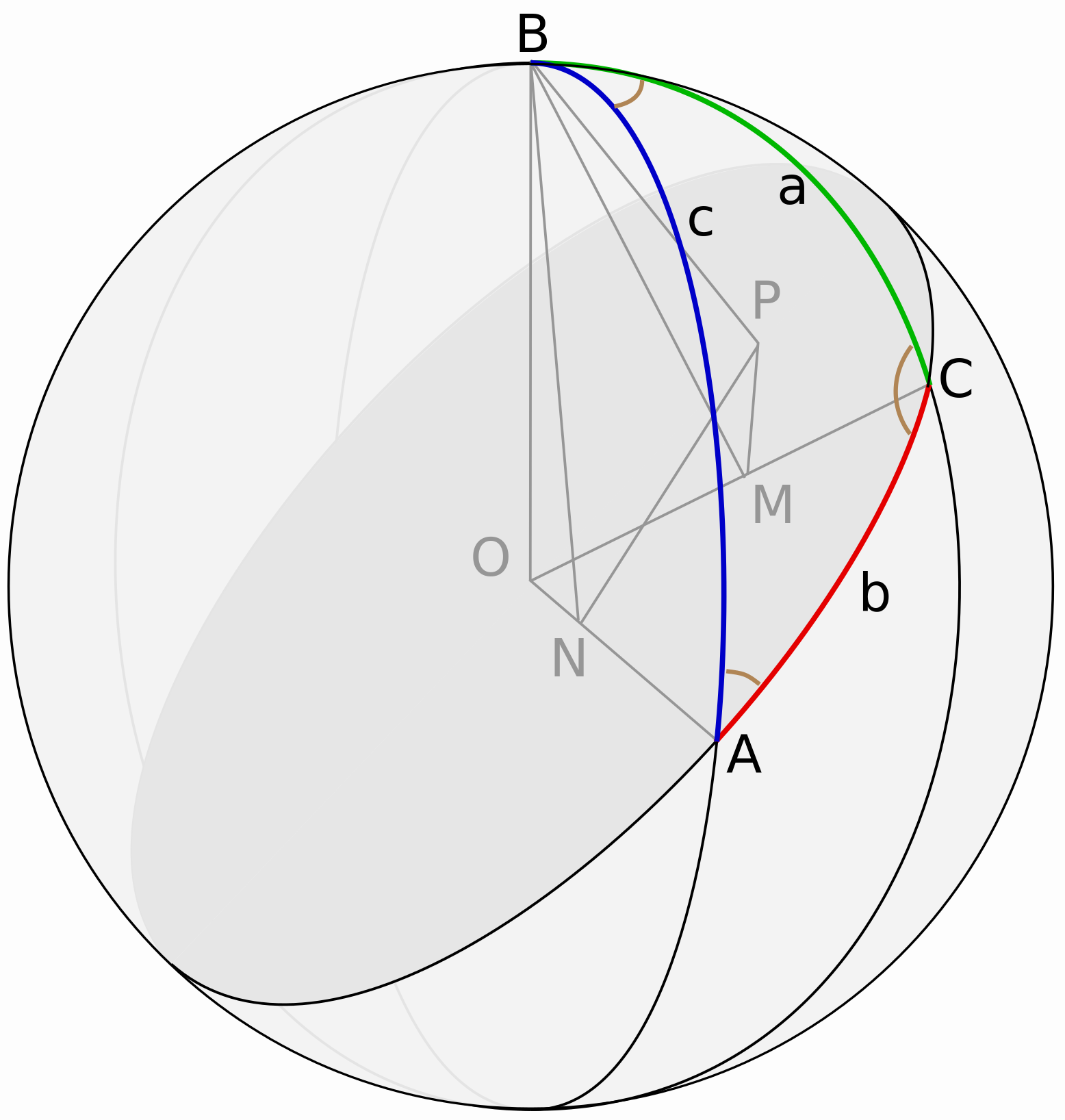
图中以$O$为圆心，半径为$R$的球体上有一个球面三角形$ABC$。$BP$垂直于通过边$b$的大圆平面，$BM$垂直于$OC$，$BN$垂直于OA。由三垂线逆定理，$PM$与$OC$垂直，$PN$与$OA$垂直。请注意，角度$MPN$等于 $b$，此外，$BM= R\sin a, BN = R\sin c$ 和 $OM = R\cos a$。接下来，我们将折线$NOMP$投影到包含$NP$的线上。
\[{\mbox{pr }}NP={\mbox{pr }}NO+{\mbox{pr }}OM+{\mbox{pr }}MP\]
\[{\mbox{pr }}NP=NP=BN\cos A=R\sin c\cos A\]
\[NO\perp NP\Rightarrow {\mbox{pr }}NO=0\]
\[{\mbox{pr }}OM=OM\cos({\frac {\pi }{2}}-\angle MON)=R\cos a\sin b\]
\[{\mbox{pr }}MP=MP\cos \angle MPN=MP\cos b=BM\cos(\pi -C)\cos b=-R\sin a\cos b\cos C\]
我们将最后四个表达式代入第一个得到：
\[\sin c\cos A=\cos a\sin b-\sin a\cos b\cos C\]