测地三角形的内角和

hbghlyj

kuing 发表于 2021-11-2 02:35
球面三角形的面积公式你知道吧？只需算三个角，也就是三个平面的夹角，这些其实都是基本东西。

Elliptic geometry
Girard's theorem: $\text{The sum of the angles of a triangle} - π = \text{the area of the triangle}$.

Proof
Take the triangle to be a spherical triangle lying in one hemisphere.

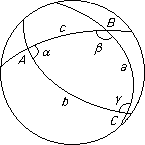
The lines $b$ and $c$ meet in antipodal points $A$ and $A'$ and they define a lune with area $2α$.

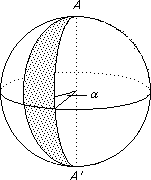
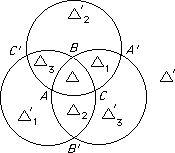
We get a picture as on the right of the sphere divided into 8 pieces with $△'$ the antipodal triangle to $△$ and $△ ∪ △_1$ the above lune, etc.

$\text{area }△ =\text{area }△'$, $\text{area }△_1 =\text{area } △'_1$,etc.

Then\begin{array}l△ + △_1 = \text{area of the lune }AA' = 2α\\
△ + △_2 =\text{area of the lune }BB'= 2β\\
△ + △_3 =\text{area of the lune }CC'= 2γ\end{array}Also $2△ + 2△_1 + 2△_2 + 2△_3 = 4π ⇒ 2△ = 2α + 2β + 2γ - 2π$ as required.

hbghlyj

从双曲几何到Gauss-Bonnet-Chern定理
描述这个差别的就是著名的（局部）Gauss-Bonnet定理，它将曲面的曲率与角盈直接联系在一起。曲面上多边形的Gauss曲率K在曲面上的积分加上多边形边界曲线的测地曲率$k_g$在边界上的积分再加上多边形外角和等于$2π$，如果这个多边形的 边界曲线是测地线，那么测地曲率就为0，这时候测地曲率的积分就为零，计算将大大简化。如果是测地三角形，那么我们马上可以得出三角形内角和公式的推广。由于内角与外角的互补关系，所以公式将变为：三角形内角和减去$π$等于Gauss曲率K在三角形所围曲面上的积分。于是我们可以知道：
如果∫K=0，那么这刚好就是平面三角形，角盈为零，三角形内角和等于$π$；
如果∫K>0，那么这就是类似于球面上的三角形，角盈为正，三角形内角和大于$π$；
如果∫K<0，那么这就是类似于伪球面上的三角形，角盈为负，三角形内角和小于$π$.

hbghlyj

人教 高中选修3-3

第24页	第25页

球面三角形的内角和是不是可以任意大?Maximum sum of angles in triangle in sphere

hbghlyj

For triangles
Hence the sum of the turning angles of the geodesic triangle is equal to $2π$ minus the total curvature within the triangle. Since the turning angle at a corner is equal to $π$ minus the interior angle, we can rephrase this as follows:

The sum of interior angles of a geodesic triangle is equal to
$π$ plus the total curvature enclosed by the triangle:

$$\sum (\pi -\alpha )=\pi +\int _{T}K.$$
In the case of the plane (where the Gaussian curvature is 0 and geodesics are straight lines), we recover the familiar formula for the sum of angles in an ordinary triangle. On the standard sphere, where the curvature is everywhere 1, we see that the angle sum of geodesic triangles is always bigger than $π$.