|
|
original poster
1+1=?
posted 2025-4-23 23:33
from mobile
Last edited by 1+1=? 2025-4-25 19:35已证明具体如图
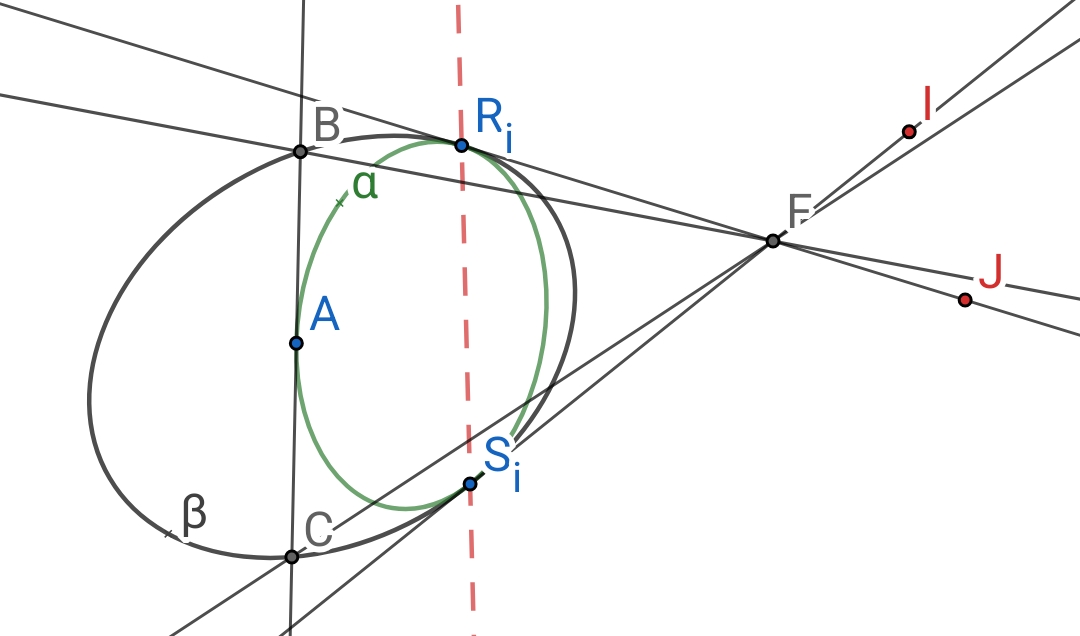
如图,$F$ 为 $\alpha$ 和 $\beta$ 的共焦点,共准线和 $\beta$ 交于两个复点 $R_i, S_i$,从 $\alpha$ 上一点 A 作切线交 $\beta$ 于 $B, C$ 二点
由于 $\alpha$ 和 $\beta$ 共焦点,又由焦点的定义(从两个圆点 $I, J$ 作四条切线所成的四个交点)可知,$\alpha, \beta$ 属于一个四线二级曲线系,即 $\alpha$ 和 $\beta$ 都和 $FI,FJ$ 相切.
又因为 $\alpha, \beta$ 共准线,即 F 分别关于 $\alpha, \beta$ 的极线与 $FI, FJ$ 的两对交切点重合,所以 $\alpha, \beta$ 又属于以 $R_i, S_i$ 为公切点的二次公切曲线系,所以点 $B, C$ 成射影对应,且 $R_i, S_i$ 二点为该射影对应的不动点,所以 $\beta$ 上 $R_i, S_i, B, C$ 四点的交比为定值 $c_i$.
因为 $F$ 为 $R_i S_i$ 的极点,所以
$(F R_i, F S_i, F B, F C)$ 也为定值 $u_i$,由焦点的定义知 $F R_i$ 和 $F S_i$ 分别过圆点,所以 $F R_i$ 和 $F S_i$ 为迷向直线,则有拉盖尔定理:
$$
\angle BFC=\frac{1}{2 i} \ln ((F R_i, FS_i, FB, FC))=\frac{1}{2 i} \ln (u_i)
$$
所以 $\angle B F C$ 为定值.
|
|