来自微信网友：1/8 球内的圆锥

kuing

问题：如图，已知球半径为 `2`，半径 `AB`, `AC`, `AF` 两两垂直，`U` 为弧 `BC` 中点，在三面角 `A`-`BCF` 与球面围成的 `1/8` 球的区域内作一个圆锥，使得顶点为 `F` 且底面中心 `Q` 在面 `AUF` 内，求该圆锥的最大体积。


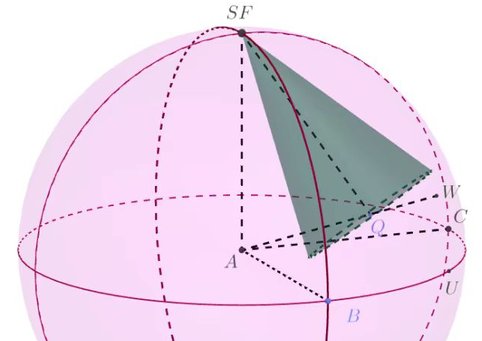
这个问题相当麻烦，几何角度似乎不好分析，于是我尝试用代数方法硬搞。

建系使球心 `A` 为原点且 `B(2,0,0)`, `C(0,2,0)`, `F(0,0,2)`，设 `Q(a,a,b)`，再设圆锥底面圆上任一点为 `P(x,y,z)`，设底面圆半径为 `r`，则有 `\abs{PQ}=r` 及 `\vv{PQ}\cdot\vv{QF}=0`，因此底面圆的方程为
\[\led
(x-a)^2+(y-a)^2+(z-b)^2&=r^2,\\
a(x-a)+a(y-a)+(b-2)(z-b)&=0,
\endled
\quad(*)\]
它得在 `1/8` 球内，因此得考查式 (*) 所确定的点的坐标范围及与原点间的距离。

先看 `z` 的最值，由图形可知，`z` 的最值必然在平面 `x=y` 上取得，于是在式 (*) 中令 `x=y` 解之即得
\begin{align*}
z_{\min}&=b-\frac{\sqrt2ar}{\sqrt{2a^2+(2-b)^2}},\\
z_{\max}&=b+\frac{\sqrt2ar}{\sqrt{2a^2+(2-b)^2}},
\end{align*}
要在 `1/8` 球内就必须满足 `z_{\min}\geqslant0`，即
\[r^2\leqslant\frac{b^2\bigl(2a^2+(2-b)^2\bigr)}{2a^2};\quad(1)\]

再看 `x` 和 `y` 的，由对称性只需看其一，需要圆与坐标平面 `xAz` 无交点或者相切，则直接在式 (*) 中令 `y=0` 并消 `z` 化简得
\[\bigl(a^2+(2-b)^2\bigr)x^2-2a\bigl(2a^2+(2-b)^2\bigr)x+4a^4+(2a^2-r^2)(2-b)^2=0,\]
那么只需上式关于 `x` 的 `\Delta\leqslant0` 即可，计算化简为
\[r^2\leqslant\frac{a^2\bigl(2a^2+(2-b)^2\bigr)}{a^2+(2-b)^2};\quad(2)\]

最后，将式 (*) 的第一式与第二式的两倍相加可得
\[x^2+y^2+z^2=2a^2+b^2-4b+r^2+4z,\]
这说明当 `z` 最大时圆上的点与原点距离最大，所以代入上面的 `z_{\max}`，即得
\[(x^2+y^2+z^2)_{\max}=2a^2+b^2+r^2+\frac{4\sqrt2ar}{\sqrt{2a^2+(2-b)^2}},\]
于是要在 `1/8` 球内就得满足
\[2a^2+b^2+r^2+\frac{4\sqrt2ar}{\sqrt{2a^2+(2-b)^2}}\leqslant4.\quad(3)\]

这样，问题就转化为：在正数 `a`, `b`, `r` 同时满足不等式 (1)(2)(3) 的情况下，求
\[V=\frac13\pi r^2\abs{QF}=\frac13\pi r^2\sqrt{2a^2+(2-b)^2}\]
的最大值。

这太复杂了，我搞不来，即便开挂上 MMA，用 Maximize 命令运行半天也出不来结果，只好改用 NMaximize 算数值解：

1. NMaximize[{1/3 Pi r^2 Sqrt[2 a^2 + (2 - b)^2],
2. r^2 <= b^2/(2 a^2) (2 a^2 + (2 - b)^2),
3. r^2 <= a^2*(2 a^2 + (2 - b)^2)/(a^2 + (2 - b)^2),
4. 2 a^2 + b^2 + r^2 + (4 Sqrt[2] a r)/Sqrt[2 a^2 + (2 - b)^2] <= 4,
5. a > 0, b > 0, r > 0}, {a, b, r}]

Copy the Code

输出：{1.34987, {a -> 0.759747, b -> 0.480506, r -> 0.832261}}

不过，凭直觉，我猜测最大值应该是当圆锥底面圆同时与三坐标平面以及球面都相切时，也就是式 (1)(2)(3) 同时取等号时，此时它们构成的方程组有唯一正数解
\[a=\frac{10-\sqrt{10}}9,\,b=\frac{-2+2\sqrt{10}}9,\,r=\frac{-2+2\sqrt{10}}{3\sqrt3},\]
代入 `V` 中化简得此时
\[V=\frac{8\pi}{729}\bigl(65\sqrt6-31\sqrt{15}\bigr)\approx1.34987124,\]
它们的近似值确实与软件输出的一样！看来应该是猜对了，只是还无法严格证明唉。

kuing

注：开头的图是提问的网友作的，我不太会作这种 3D 图。
有哪位帮我作个 3D 图验证一下，看看后面我算的那个 a, b, r 值是否使得圆锥同时与三坐标平面以及球面都相切，以及体积是不是那个数值？

hbghlyj

kuing

hbghlyj 发表于 2023-5-16 17:02

多谢😊

PS、在 asymptote.ualberta.ca/ 里输入你这图的代码，就可以得到能拖动的 3D 图，看起来确实是都相切的😊

kuing

提问者提议把题改简单一点，仅求底面圆与三面角及球面均相切时的半径大小，但我也想不出什么简单的计算方法，唉😔

依旧建系使球心 `A` 为原点且 `B(2,0,0)`, `C(0,2,0)`, `F(0,0,2)`，设底面圆与面 `ABC` 及球面分别切于 `D`, `E`，显然这两点均在面 `AUF` 内，所以可设 `D(2c,2c,0)`, `E(2d,2d,2e)`，其中 `c`, `d`, `e\in(0,1)`，那么底面圆的圆心 `Q(c+d,c+d,e)`。

由 `E` 在球面上得
\[2d^2+e^2=1,\quad(1)\]
由 `FD=FE` 及上式有
\[2c^2+1=2d^2+(e-1)^2=1-e^2+(e-1)^2=2-2e,\]
即
\[2c^2=1-2e,\quad(2)\]
由式 (1)(2) 得
\[2(c^2+d^2)=2-2e-e^2,\quad(3)\]
设底面圆半径为 `r`，母线长为 `l`，则
\begin{align*}
r^2&=\frac{DE^2}4=2(c-d)^2+e^2=2-2e-4cd,&&(4)\\
l^2&=FD^2=8c^2+4=4(1-2e)+4=8(1-e),&&(5)
\end{align*}
设圆锥的半顶角为 `\theta`，由于圆锥与面 `FAC` 相切，则圆锥的对称轴 `FQ` 与面 `FAC` 所成角 `=\theta`，因此 `FQ` 与 `x` 轴的夹角为 `90\du-\theta`，而 `\vv{FQ}=(c+d,c+d,e-2)`，记 `\vec x=(1,0,0)`，于是有
\begin{align*}
\sin\theta=\cos\langle\vv{FQ},\vec x\rangle
&\iff\frac rl=\frac{c+d}{\abs{FQ}}\\
&\iff\frac{r^2}{l^2}=\frac{(c+d)^2}{l^2-r^2},
\end{align*}
代入式 (3)(4)(5) 化简得到
\[\frac{1-e-2cd}{1-e}=\frac{2-2e-e^2+4cd}{3-3e+2cd},\]
去分母整理为
\[4(cd)^2+8(1-e)cd+(e-1)(e^2-e+1)=0,\quad(6)\]
又由式 (1)(2) 有
\[4(cd)^2=(1-2e)(1-e^2),\quad(7)\]
代入式 (6) 后约去 `(1-e)` 即
\[(1-2e)(1+e)+8cd-(e^2-e+1)=0,\]
化简为
\[8cd=3e^2,\]
再两边平方代入式 (7) 得
\begin{align*}
&16(1-2e)(1-e^2)=9e^4\\
\iff{}&(e-2)^2(9e^2+4e-4)=0\\
\riff{}&e=\frac{-2+2\sqrt{10}}9,
\end{align*}
那么
\[cd=\frac38e^2=\frac{11-2\sqrt{10}}{54},\]
代回式 (4) 即
\[r^2=2-2e-4cd=\frac4{27}\bigl(11-2\sqrt{10}\bigr)=\frac4{27}\bigl(\sqrt{10}-1\bigr)^2,\]
所以
\[r=\frac2{3\sqrt3}\bigl(\sqrt{10}-1\bigr).\]

kuing

平放圆柱：



如图，设球半径为 `R`，圆柱底面圆半径为 `r`，则 `AO=\sqrt2r`，那么圆柱的高为
\[h=\sqrt{R^2-(AO+r)^2}=\sqrt{R^2-\bigl(\sqrt2+1\bigr)^2r^2},\]
设圆柱的体积为 `V`，有
\begin{align*}
V&=\pi r^2h=\pi r^2\sqrt{R^2-\bigl(\sqrt2+1\bigr)^2r^2}\\
&=\frac{2\pi}{\bigl(\sqrt2+1\bigr)^2}\sqrt{\frac12\bigl(\sqrt2+1\bigr)^2r^2\cdot\frac12\bigl(\sqrt2+1\bigr)^2r^2\cdot\Bigl(R^2-\bigl(\sqrt2+1\bigr)^2r^2\Bigr)}\\
&\leqslant\frac{2\pi}{\bigl(\sqrt2+1\bigr)^2}\sqrt{\left(\frac{R^2}3\right)^3}\\
&=\frac{6\sqrt3-4\sqrt6}9\pi R^3,
\end{align*}
当 `r=\frac{2\sqrt3-\sqrt6}3R` 时取等。

设圆柱的表面积为 `S`，有
\[S=2\pi r^2+2\pi rh=2\pi r^2+2\pi r\sqrt{R^2-\bigl(\sqrt2+1\bigr)^2r^2},\]
为方便书写记 `u=\bigl(\sqrt2+1\bigr)^2`，令 `f(r)=r^2+r\sqrt{R^2-ur^2}`，则
\[f'(r)=2r+\frac{R^2-2ur^2}{\sqrt{R^2-ur^2}},\]
令 `f'(r)=0` 解得
\[r^2=\frac{R^2}{2u}\left(1+\frac1{\sqrt{1+u}}\right),\]
代回去化简再把 `u` 的值也代入化简可得
\begin{align*}
f(r)_{\max}&=\frac{1+\sqrt{1+u}}{2u}R^2,\\
&=\frac{3-2\sqrt2+\sqrt{20-14\sqrt2}}2R^2,
\end{align*}
所以
\[S_{\max}=\left(3-2\sqrt2+\sqrt{20-14\sqrt2}\right)\pi R^2,\]
当 `r=\frac12\sqrt{6-4\sqrt2+\sqrt{58-41\sqrt2}}\cdot R` 时取等。

---

斜放圆柱的一种好算的情况：



如图，圆柱的两个底面圆，一个在球面上，另一个与三个坐标平面均相切，且直线 `O_1O_2` 与三坐标轴的夹角相同。

设底面圆半径为 `r`，圆柱高为 `h`，设 `AO_1=m`，先求 `m` 与 `r` 的关系。

设圆 `O_1` 所在平面与 `AB`, `AC`, `AD` 分别交于 `B_1`, `C_1`, `D_1`，则不难求出 `AB_1=AC_1=AD_1=\sqrt3m`，那么 `\triangle B_1C_1D_1` 是边长为 `\sqrt6m` 的正三角形，而圆 `O_1` 就是其内切圆，所以 `2\sqrt3r=\sqrt6m`，得到
\[m=\sqrt2r,\]
设球的半径为 `R`，则 `(m+h)^2+r^2=R^2`，所以
\[h=\sqrt{R^2-r^2}-\sqrt2r,\]
由 `h>0` 得 `r<R/\sqrt 3`，设圆柱的体积为 `V`，则
\[V=\pi r^2h=\pi r^2\bigl(\sqrt{R^2-r^2}-\sqrt2r\bigr),\]
令 `f(r)=r^2\bigl(\sqrt{R^2-r^2}-\sqrt2r\bigr)`，求导有
\[f'(r)=\frac{2R^2r-3r^2}{\sqrt{R^2-r^2}}-3\sqrt2r^2,\]
令
\[f'(r)=0\riff r=\frac13\sqrt{5-\sqrt{13}}R,\]
代回去化简得
\[V_{\max}=\frac19\sqrt{94-26\sqrt{13}}\pi R^3,\]
在数值上比前面正放的要小。

至于表面积 `S`，有
\[S=2\pi r^2+2\pi rh=2\pi r\Bigl(\sqrt{R^2-r^2}-\bigl(\sqrt2-1\bigr)r\Bigr),\]
然后也是求导算最值，就不细写了，结果是：当 `r=\frac12\sqrt{2-\sqrt{2-\sqrt2}}R` 时
\[S_{\max}=\left(1-\sqrt2+\sqrt{4-2\sqrt2}\right)\pi R^2,\]
数值上比前面正放的要大！！😃（此时这圆柱非常扁）

---

斜放圆柱的另一种情况：	横放圆柱：

这两种情况光看起来就知道相当复杂，有空再说吧……

待续…………

kuing

正放长方体：



如图，设 `FE=a`, `FG=b`, `FF_1=c`, `\angle EFA=\theta`，不妨设 `\theta\in[0,45\du]`，则只需确保 `G_1` 在球面上即可。

设球半径为 `R`，建系使 `AB`, `AC`, `AD` 为 `x`, `y`, `z` 轴，则易知 `G_1(a\cos\theta+b\sin\theta,b\cos\theta,c)`，所以
\[(a\cos\theta+b\sin\theta)^2+(b\cos\theta)^2+c^2=R^2,\]
即
\[a^2\cos^2\theta+b^2+2ab\sin\theta\cos\theta+c^2=R^2,\]
长方体体积 `V=abc`，则由均值有
\begin{align*}
R^2&\geqslant2ab\cos\theta+2ab\sin\theta\cos\theta+c^2\\
&=ab\cos\theta(1+\sin\theta)+ab\cos\theta(1+\sin\theta)+c^2\\
&\geqslant3\sqrt[3]{a^2b^2c^2\cos^2\theta(1+\sin\theta)^2}\\
&=3\sqrt[3]{V^2\cos^2\theta(1+\sin\theta)^2},
\end{align*}
所以
\[V\leqslant\frac{\sqrt3}{9\cos\theta(1+\sin\theta)}R^3,\]
不难证明当 `\theta\in[0,45\du]` 时 `\cos\theta(1+\sin\theta)\geqslant1`，所以
\[V\leqslant\frac{\sqrt3}9R^3,\]
当 `\theta=0` 且 `a=b=c=R/\sqrt3` 时取等。

也就是说这种摆放方法一定是当长方体三个侧面在三个坐标平面上而且是正方体时体积最大。

至于表面积，有空再算吧……

---

斜放长方体：



想想就困难，也是有空再说吧……

待续…………

kuing

正放正三棱锥：



如图，正三棱锥 `G`-`AEF` 的底面在平面 `ABC` 上，设球半径为 `R`，`O` 为正 `\triangle AEF` 的中心，设 `AO=m`，则正 `\triangle AEF` 的边长为 `\sqrt3m`，它不能超过球面，所以 `\sqrt3m\leqslant R`，即 `m^2\in[0,R^2/3]`，而 `\S{AEF}=\frac{3\sqrt3}4m^2`，三棱锥的高 `h=\sqrt{R^2-m^2}`，所以体积
\[V=\frac13\S{AEF}h=\frac{\sqrt3}4m^2\sqrt{R^2-m^2},\]
令
\begin{align*}
f(x)&=x\sqrt{R^2-x},\quad x\in\left[0,\frac13R^2\right],\\
f'(x)&=\frac{2R^2-3x}{2\sqrt{R^2-x}}>0,\\
\riff V_{\max}&=\frac{\sqrt3}4f\left(\frac13R^2\right)=\frac{\sqrt2}{12}R^3,
\end{align*}
当 `m^2=R^2/3`（即 `E`, `F` 在球面上）时取等。

其实从实际上来说，正三棱锥的话，要体积最大，应该让 `\triangle EFG` 为底，即改为正三棱锥 `A`-`EFG`，这时显然是当 `EFG` 分别在 `BCD` 处时体积最大为 `R^3/6`。


表面积的话，应该也不难，不想写了…………

kuing

听说今天高考考了这样一道题：


O(∩_∩)O哈！还别说，这跟上面玩的东西算是想到一块去了，那微信网友可以算是押中了题。当然正方体简单一些，但至少思路有那么点像，也是考虑斜放的（D）。

kuing

作一平面斜截正方体，使截面为正六边形，那么该正六边形的中心 `O` 也就是正方体的中心。

不难求出这个正六边形的内切圆直径为 `\sqrt6/2\approx1.22`，这说明该正六边形能够套住直径为 `1.2` 的圆柱。

现在这样放置圆柱：让圆柱的中心在 `O` 处且两底面与正六边形所在平面平行，如图所示：

（只是示意图，不是完全按原数据画的，因为数据太接近，按原数据画会看不清）

看到网上有些答案写到这里就直接说 D 正确了，其实还未够严谨。

虽然正六边形能套住圆柱并且圆柱高 `0.01` 很薄，但正六边形内切圆直径也只不过比圆柱直径大 `0.02` 多一点，所以相对来说，圆柱这高并不能忽略不计，有没有超出正方体还是需要论证一下的。

如图所示，过 `O` 作正六边形一边的垂线 `OP` 交圆柱侧面于 `Q`，在 `\triangle OPA` 中，过 `Q` 作 `OP` 的垂线交 `PA` 于 `R`，要证明圆柱没有超出正方体，只需证明 `QR\geqslant0.005`。

易知 `OA=\sqrt3/2`, `OP=\sqrt6/4`，记 `OQ=r`，则
\[QR=PQ\cdot\frac{OA}{OP}=\left(\frac{\sqrt6}4-r\right)\cdot\sqrt2=\frac{\sqrt3}2-\sqrt2r,\]
代入题中 `r=0.6`，即
\[QR=\frac{\sqrt3}2-\frac35\sqrt2\approx0.017>0.005,\]
所以它确实没超出正方体。

isee

kuing 发表于 2023-6-9 02:13
作一平面斜截正方体，使截面为正六边形，那么该正六边形的中心 `O` 也就是正方体的中心。

不难求出这个正 ...

越看越像蛋糕