|
|
 kuing
kuing
posted 2023-11-13 15:38
Last edited by kuing 2023-11-13 15:46命题:给定圆锥曲线 Γ,定点 P、Q,过 P 的动直线与 Γ 交于 A、B,直线 QA、QB 交 Γ 于另外两点 M、N,直线 MN 与 PQ 交于 R,则 R 为定点。
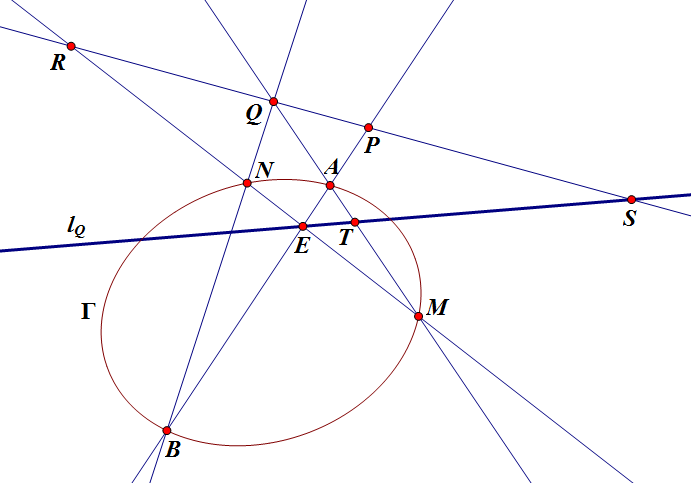
极点极线解释:
如图,设 Q 的极线为 `l_Q`,则 AB 与 MN 的交点 E 在 `l_Q` 上,设 `l_Q` 与 PQ 交于 S,与 AM 交于 T,则 Q、A、T、M 调和,则 EQ、EA、ET、EM 与 RS 的四交点 Q、P、S、R 调和,因此当 P、Q 为定点时,S 是定点,所以 R 也是定点。
回到原题,AM、BN 斜率都是 2,可以看成上述命题的 Q 为无穷远点且 `y_Q:x_Q\to2`,那么:
极线 `l_Q` 就是 y=2x 的共轭直径 y=-x/8;
直线 PQ 就是过 P(1,1) 且斜率为 2 的直线 y=2x-1,
联立 y=-x/8 与 y=2x-1 得交点 S(8/17,-1/17),
而 Q 无穷远则 S 为 PR 中点,所以 R(-1/17,-19/17),这就是最终所求的定点。
|
|