摆线演示

kuing

1. R := 4;
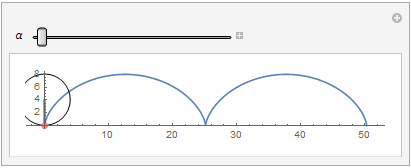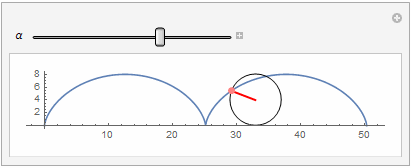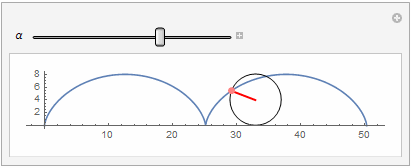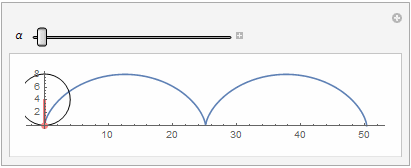
2. Manipulate[
3. Show[ParametricPlot[{\[Alpha] R + R Cos[-(\[Pi]/2) - \[Alpha]],
4.      R + R Sin[-(\[Pi]/2) - \[Alpha]]}, {\[Alpha], 0, 4 \[Pi]}] //
5.    Evaluate,
6.   Graphics[{Circle[{\[Alpha] R, R}, R], Red, Thick,
7.     Line[{{\[Alpha] R + R Cos[-(\[Pi]/2) - \[Alpha]],
8.        R + R Sin[-(\[Pi]/2) - \[Alpha]]}, {\[Alpha] R, R}}],
9.     PointSize[Large], Pink,
10.     Point[{\[Alpha] R + R Cos[-(\[Pi]/2) - \[Alpha]],
11.       R + R Sin[-(\[Pi]/2) - \[Alpha]]}]}]], {\[Alpha], 0, 4 \[Pi]}]

Copy the Code

转自：math.org.cn/forum.php?mod=redirect&goto=f … 37985&pid=174408
PS、该帖“板凳”的计算方法也是经典。

isee

的确是厉害。。。。。

kuing

那边将要关闭了，把“板凳”的计算方法也引用过来存个档吧……

月出孤舟寒  发表于 2017-11-18 17:38:37

从运动学的角度来做无需写出摆线方程

如图，假设半径为 $R$ 的圆沿直线做无滑滚动，转动角速度为 $\omega $

由于是无滑，所以 $P$ 点速度 $\upsilon \bot PB$ 从而 $\upsilon=\omega\overline{PB} =\omega 2R\sin \frac{\theta}{2}$

从而 $\mathrm{d}s=\upsilon\mathrm{d}t=2\omega R\sin \frac{\theta}{2}\mathrm{d}t=2R\sin \frac{\theta}{2}\mathrm{d}\theta$

所以一轮摆线的长度就是 $\int_0^{2\pi}2R\sin \frac{\theta}{2}\mathrm{d}\theta=8R$