斜率乘积，斜率和，斜率比值是定值产生定点的背景？

Tesla35

斜率乘积是定值
已知点$P$是圆$x^2+y^2=1$上任意一点,过点$P$作$y$轴的垂线,垂足为$Q$,点$R$满足$\vv{RQ}=\sqrt{3}\vv{PQ}$,记点$R$的轨迹为曲线$C$.
(1)求曲线$C$的方程;
(2)设$A(0,1)$,点$M,N$在曲线$C$上,且直线$AM$与直线$AN$的斜率之积为$\frac{2}{3}$.
(i)证明:直线$MN$过定点;
(ii)求$\triangle AMN$的面积的最大值.

斜率和是定值
已知$F(1,0)$,$P$是平面上一动点,$P$到直线$l:x=-1$上的射影为点$N$,且满足$(\vv{PN}+\frac{1}{2}\vv{NF})\cdot\vv{NF}=0$.
(1)求点$P$的轨迹$C$的方程;
(2)过点$M(1,2)$作曲线$C$的两条弦$MA,MB$,设$MA,MB$所在直线的斜率分别为$k_1,k_2$,当$k_1,k_2$变化且满足$k_1+k_2=-1$时,证明直线$AB$恒过定点,并求出该定点坐标.

斜率比值是定值
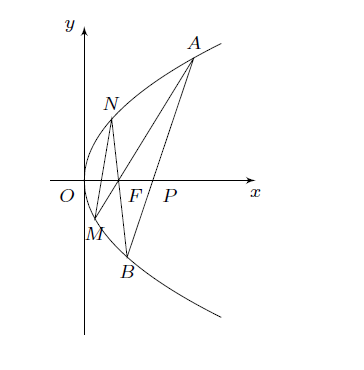
如图,已知抛物线$y^2=4x$的焦点为$F$.过点$P(2,0)$的直线交抛物线于$A(x_1,y_1),B(x_2,y_2)$两点,直线$AF,BF$分别与抛物线交于点$M,N$.
(1)求$y_1y_2$的值;
(2)记直线$MN$的斜率为$k_1$,直线$AB$的斜率为$k_2$.证明:$\frac{k_1}{k_2}$为定值.



这类题目是否有高等背景？

kuing

怎么全是 \\ ……
话说，第一问答案给一下啊

kuing

斜率之和为定值，一搜就有了：forum.php?mod=viewthread&tid=5937

kuing

斜率之积：forum.php?mod=viewthread&tid=626

kuing

咦？又多了个斜率之比？没问题，也有：forum.php?mod=viewthread&tid=5384

kuing

昨晚讨论组里的一题：

与楼主的第三题是一样的，也放这里好了。

事实上，可以更一般化一点：

如上图，圆锥曲线 `\Gamma` 的对称轴为 `x` 轴，`M`, `N` 是 `x` 轴上两定点，`\Gamma` 上的弦 `AB` 过 `M`，弦 `AC`, `BD` 过 `N`，则：
（1）直线 `CD` 与 `x` 轴的交点为定点；
（2）直线 `CD` 与 `AB` 的斜率之比为定值。

证明：把图形画成如下图那样。

则 `ST` 是 `N` 的极线，垂直于 `x` 轴，且 `M`, `N`, `P`, `Q` 调和，从而 `P` 是定点，以及 `k_{CD}:k_{AB}=(SQ/QP):(SQ/QM)=QM:QP=MN:NP` 为定值，QED。

回到昨晚讨论组里那题，即 `\Gamma`: `x^2/4+y^2/3=1`，`M` 为原点，`N` 为焦点 `(1,0)`，易知此时 `Q(4,0)` 且 `P(8/5,0)`，所以 `k_{CD}:k_{AB}=1:(8/5-1)=5/3`。

而回到楼主的第三题，即 `\Gamma`: `y^2=4x`, `M(2,0)`, `N(1,0)`，易知此时 `Q(-1,0)` 且 `P(0.5,0)`，所以 `k_{CD}:k_{AB}=1:0.5=2`。

lemondian

回复 6# kuing
@kunig:在第3个图中，过点N作直线垂直于x轴，交AB于点E，交CD于点F，则NE=NF，如果能证明这个结论。则可不要调和的知识了吧？
在ggb中，NE=NF是对的，但我不会证。是不是与蝴蝶定理有点关系？

kuing

回复 7# lemondian

那本来就是蝴蝶定理……

lemondian

回复 8# kuing

交点E, F在曲线外，如何用蝴蝶定理？@kuing请写一下吧！

kuing

回复 9# lemondian

蝴蝶定理分内外的吗？

kuing

回复 9# lemondian

看这帖吧 forum.php?mod=viewthread&tid=399 ，帖中 7# 的解析法你应该能看得懂，该证法清楚显示根本没什么内外之分。

lemondian

回复 11# kuing
看了一下，那边的方法应该看懂了！
但这边还是卡了，过不来。。。

lemondian

如上图，圆锥曲线$\Gamma$ 的对称轴为$x$轴，$M,N$ 是$x$ 轴上两定点，$\Gamma$上的弦$AB$过$M$，弦$AC$, $BD$过$N$，则：
（1）直线$CD$与$x$轴的交点为定点，并求出定点坐标；
（2）直线$CD$与$AB$的斜率之比为定值;
（3）直线$AD$与$BC$的交点轨迹为$x=\dfrac{a^2}{n}$;
(4)$(k_{AD}+k_{BC})k_{AB}=\dfrac{2b^2}{mn-a^2}$

lemondian

回复 2# kuing
@kuing:
呵呵，我就是从你哪盗图过来的！
我看懂了你的调和做法。（原贴没有问题3，问题4，也不会用调和方法搞）
但想用一般的解几方法来做，几番努力，算出了问题（2），但另外3个问题没有解决。
求助大家，如何解几方法解决？

kuing

回复 3# lemondian

那里的证明实际上就包含了（3），至于（4）有空再看。

lemondian

回复 4# kuing
@kuing:有空看看问题（4）吗？

kuing

又见一个斜率之比，记录一下吧：

点 `P(-5,0)`，圆 `C`: `(x-1)^2+y^2=4`，过原点的直线与圆 `C` 交于 `M`, `N` 两点，直线 `PM` 与圆 `C` 的另一个交点为 `R`，直线 `PN` 与圆 `C` 的另一个交点为 `S`，记直线 `MN` 和直线 `RS` 的斜率分别为 `k_1`, `k_2`，求证 `k_2/k_1` 为定值。

用曲线系的方法：依题意可设以下直线方程
\begin{align*}
MN\colon && y-k_1x&=0,\\
RS\colon && y-k_2x+m&=0,\\
PM\colon && y+s(x+5)&=0,\\
PN\colon && y+t(x+5)&=0,
\end{align*}
则存在实数 `\lambda`, `\mu` 使得
\begin{align*}
&\lambda(y-k_1x)(y-k_2x+m)+\mu\bigl((x-1)^2+y^2-4\bigr)\\
={}&\bigl(y+s(x+5)\bigr)\bigl(y+t(x+5)\bigr),
\end{align*}
比较两边的 `xy` 项和 `y` 项的系数，有
\[\led
-\lambda(k_1+k_2)&=s+t,\\
\lambda m&=5t+5s
\endled
\riff m=-5(k_1+k_2),\]
再比较 `x^2` 项和 `x` 项的系数以及常数项，有
\[\led
\lambda k_1k_2+\mu&=st,\\
-\lambda k_1m-2\mu&=10st,\\
-3\mu&=25st,
\endled\]
消 `st` 得
\begin{align*}
\led
-\lambda k_1(m+10k_2)&=12\mu,\\
-25\lambda k_1k_2&=28\mu
\endled
&\riff\frac{m+10k_2}{25k_2}=\frac37\\
&\riff k_2=\frac75m=-7(k_1+k_2)\\
&\riff\frac{k_2}{k_1}=-\frac78.
\end{align*}