两个眼熟的椭圆结论

力工

此问题怎么看怎么眼熟，觉得可以从椭圆的性质出发用综合法破解，但本人脑力着急，只会解析法，联系不上性质。想求大佬们指点。
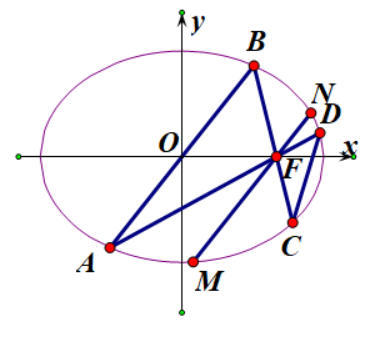
椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的一个焦点为$F$,凹四边形的边$AB$过原点$O$,边$BC,AD$过点$F$,且过$F$的直线$MN//AB$,证明：
（1）$\frac{k_{CD}}{ k_{AB}}=\frac{1+e^2}{1-e^2}$.
(2)$|AB|^2=2a\cdot |MN|$.

kuing

（1）是斜率之积？印象中应该是之比才是定值吧

kuing

（1）就不玩了，写一下（2）好了：
设 `AB` 倾斜角为 `\theta` 以及 `AB=2r`，则 `B(r\cos\theta,r\sin\theta)`，代入椭圆中得
\[\frac{r^2\cos^2\theta}{a^2}+\frac{r^2\sin^2\theta}{b^2}=1,\]
所以
\[AB^2=4r^2=\frac{4a^2b^2}{a^2\sin^2\theta+b^2\cos^2\theta},\]
至于 `MN`，用圆锥曲线的极坐标方程易得
\[MN=\frac{ep}{1+e\cos\theta}+\frac{ep}{1-e\cos\theta}=\frac{2ep}{1-e^2\cos\theta},\]
代入 `e=c/a` 以及 `p=a^2/c-c=b^2/c` 化简上式为
\[MN=\frac{2ab^2}{a^2-c^2\cos\theta}=\frac{2ab^2}{a^2\sin^2\theta+b^2\cos^2\theta},\]
所以 `AB^2=2a\cdot MN`。