椭圆，过焦点斜率相反，两线之差为定值

kuing

前几天微信网友发来的题，貌似是最近的模拟题：

在平面直角坐标系 $x O y$ 中，点 $A(-1,0), B(1,0), Q(-4,0)$，动点 $P$ 满足 $P A+P B=4$，记点 $P$ 的轨迹为 $C$．
（1）求 $C$ 的方程；
（2）过点 $Q$ 且斜率不为 0 的直线 $l$ 与 $C$ 相交于两点 $E, F$（ $E$ 在 $F$ 的左侧）．设直线 $A E, A F$ 的斜率分别为 $k_1, k_2$．
①求证：$\frac{k_1}{k_2}$ 为定值；
②设直线 $A F, B E$ 相交于点 $M$，求证：$M A-M B$ 为定值．

（1）略；（2）①易证 `k_1+k_2=0`；

将第②问单独成一题，就是：

如下图，椭圆 `x^2/a^2+y^2/b^2=1`（`a>b>0`），`A`, `B` 是焦点，`AE` 与 `AF` 斜率互反，`AF` 交 `BE` 于 `M`，求证 `MB-MA` 为定值。

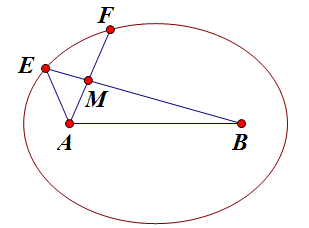
几何味很浓，不知有没有能完全脱离椭圆的纯几何证法呢

我下面的证法还需要用到一点椭圆中的公式。

证明：设 `\angle MAB=\theta`，则 `\angle EAB=\pi-\theta`, `\angle EAM=\pi-2\theta`，一方面有
\[\frac{MB}{EB}=\frac{\S{MAB}}{\S{EAB}}=\frac{AB\cdot AM\cdot\sin\theta}{AB\cdot AE\cdot\sin(\pi-\theta)}=\frac{AM}{AE},\]
即
\[\frac{MB}{MA}=\frac{EB}{EA}=\frac{2a}{EA}-1,\]
得到
\[MB-MA=2MA\left(\frac a{EA}-1\right),\]
另一方面有
\begin{align*}
&\S{AMB}+\S{AME}=\S{ABE}\\
\iff{}& AM\cdot2c\sin\theta+AM\cdot AE\cdot\sin(\pi-2\theta)=2c\cdot AE\cdot\sin(\pi-\theta)\\
\iff{}& AM=\frac{c\cdot AE}{c+AE\cos\theta},
\end{align*}
代入上面得
\[MB-MA=\frac{2c\cdot AE}{c+AE\cos\theta}\left(\frac a{EA}-1\right)=2c\cdot\frac{a-AE}{c+AE\cos\theta},\]
设 `E(x_0,y_0)`，则由焦半径公式有
\[AE=a+ex_0,\]
又由几何意义知
\[AE\cos\theta=-c-x_0,\]
代入上面即得
\[MB-MA=2c\cdot\frac{-ex_0}{-x_0}=2ce.\]

kuing

由此结果看，应该可以抽出如下初中几何题目来：

如图，在钝角 `\triangle ABC` 中，`\angle CAB` 为钝角，`D` 在 `BC` 上满足 `\angle DAB+\angle CAB=180\du`，求证：
\[DB-DA=\frac{AB^2}{CA+CB}.\]

证出它即实现原题脱离椭圆。

kuing

设 `BC=a`, `CA=b`, `AB=c`, `DB=x`, `DA=y`，类似 1# 有
\[\frac xa=\frac{\S{DAB}}{\S{CAB}}=\frac{yc\sin\angle DAB}{bc\sin\angle CAB}=\frac yb,\]
设
\[\frac xa=\frac yb=k,\]
由斯特瓦尔特定理有
\[y^2=\frac{b^2x+c^2(a-x)}a-x(a-x),\]
所以
\[k^2b^2=kb^2+c^2(1-k)-k(1-k)a^2,\]
化简得
\[k(a^2-b^2)=c^2,\]
即
\[(x-y)(a+b)=c^2,\]
即得证。

用了斯特瓦尔特定理，感觉还是不够漂亮……还有没有更初中的证法呢🤔

kuing

生如夏花  16:39
相似三角形
在线段DB上截取DM=y，在BC延长线上截取CN=b，导角得△BMA∽△BAN
@kuing 是你最后那个式子，提示必须相似，我想了几天都在椭圆里想，还以为是椭圆的某个几何性质没发现呢

（我只是写个完整过程兼画个图）

如图，在线段 `DB` 上截取 `DM=DA`，在 `BC` 延长线上截取 `CN=CA`，则有
\begin{align*}
2\angle N&=\angle ACB\\
&=180\du-\angle CAB-\angle B\\
&=\angle DAB-(\angle DMA-\angle MAB)\\
&=\angle DAB-\angle DAM+\angle MAB\\
&=2\angle MAB,
\end{align*}
所以 `\angle N=\angle MAB`，即得 `\triangle BMA\sim\triangle BAN`，所以有
\[DB-DA=BM=\frac{AB^2}{BN}=\frac{AB^2}{CA+CB}.\]

1+1=？

参见2012年浙江那个椭圆题