|
|
 kuing
kuing
posted 2024-9-22 04:50
Last edited by kuing 2024-9-22 05:02最后的②挺好玩,不妨整个一般数字的结论:
设 `F_1(-c,0)`, `F_2(c,0)`, `c>0`,两个椭圆 `\Gamma_1`, `\Gamma_2` 均以 `F_1`, `F_2` 为焦点,半长轴分别为 `a_1`, `a_2`,其中 `a_1>a_2>c`,动点 `Q(x_0,y_0)` 在 `\Gamma_2` 上且 `y_0>0`,记直线 `QF_1` 与 `\Gamma_1` 在 `x` 轴上方的交点为 `A(x_1,y_1)`,直线 `QF_2` 与 `\Gamma_1` 在 `x` 轴上方的交点为 `B(x_2,y_2)`,求 `y_0`, `y_1`, `y_2` 之间的关系。
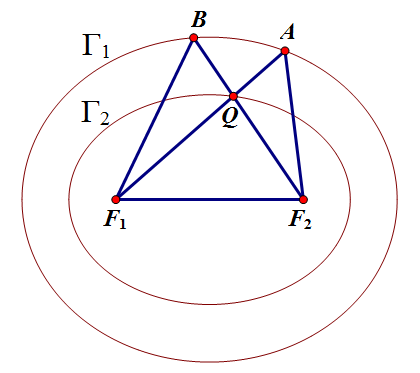
记 `\Gamma_1`, `\Gamma_2` 的离心率分别为 `e_1`, `e_2`,先看线段 `AQF_1`,有
\[\frac{y_0}{y_1}=\frac{x_0+c}{x_1+c}=\frac{QF_1}{AF_1}=\frac{a_1+e_1x_0}{a_2+e_2x_1},\]
则由等比定理得
\[\frac{x_0+c}{x_1+c}=\frac{a_1+e_1x_0-e_2(x_0+c)}{a_2+e_2x_1-e_2(x_1+c)}=\frac{a_1+(e_1-e_2)x_0-e_2c}{a_2-e_2c},\]
代入 `e_1=c/a_1`, `e_2=c/a_2` 化简得
\[\frac{y_0}{y_1}=\frac{x_0+c}{x_1+c}=\frac{a_1^2a_2-c(a_1-a_2)x_0-a_1c^2}{a_1(a_2^2-c^2)},\]
同理,对于线段 `BQF_2`,即以上结论的 `c` 变成 `-c`,因此必然有
\[\frac{y_0}{y_2}=\frac{a_1^2a_2+c(a_1-a_2)x_0-a_1c^2}{a_1(a_2^2-c^2)},\]
以上两式相加即得
\[\frac{y_0}{y_1}+\frac{y_0}{y_2}=\frac{2(a_1a_2-c^2)}{a_2^2-c^2}.\]
回到原题,即 `c=1`, `a_1=2`, `a_2=3/2`,结论即为
\[\frac1{y_1}+\frac1{y_2}=\frac43\cdot\frac1{y_0}.\]
(看来命题者设第①小问的目的是提示第②小问的关系也是类似的样子) |
|