SL(2,ℤ)

hbghlyj

[UTM] M. A. Armstrong, groups and symmetry

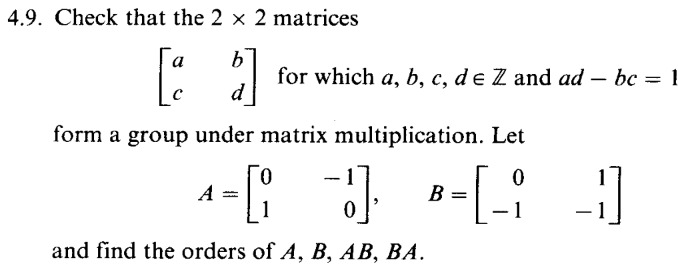
4.9. Check that the $2 \times 2$ matrices$$\left[\begin{array}{ll}a & b \\c & d\end{array}\right] \text { for which } a, b, c, d \in \mathbb{Z} \text { and } a d-b c=1$$form a group under matrix multiplication. Let$$A=\left[\begin{array}{rr}0 & -1 \\1 & 0\end{array}\right], \quad B=\left[\begin{array}{rr}0 & 1 \\-1 & -1\end{array}\right]$$and find the orders of $A, B, A B, B A$.

我们可以用 Magma 检查

1. SL2 := SL(2, Integers());
2. A := SL2![[0, -1], [1, 0]];
3. B := SL2![[0, 1], [-1, -1]];
4. Order(A);
5. Order(B);
6. A*B;
7. B*A;

复制代码

$\text{Order}(A)=4$
$\text{Order}(A)=3$
$AB=\pmatrix{1&1\\0&1}$
$BA=\pmatrix{1&0\\-1&1}$
因此 $\text{Order}(AB),\text{Order}(BA)$ 都是无限。
Modular group Presenting as a matrix group