笛沙格对合定理的对偶

hbghlyj

从 纯几何吧 搬来一帖子：

一个点与一个完全四线形的三双对顶点的连线和从该点向内切于该 四线形的圆锥曲线所引的切线构成一个对合的四个射线偶。

又见AoPS On the Desargues' Involution Theorem

Theorem 2.5 (Dual of Desargues' Involution Theorem). Let $P, A, B, C, D$ be points on a plane with $\overline{A B} \cap \overline{C D}=E, \overline{A D} \cap \overline{B C}=F$. Let a conic $\mathcal{C}$ tangent to lines $A B, C D, A D, B C$. Let $\overline{P X}, \overline{P Y}$ are the tangent line from $P$ to $\mathcal{C}$. Then $(\overline{P X}, \overline{P Y}),(\overline{P A}, \overline{P C}),(\overline{P B}, \overline{P D}),(\overline{P E}, \overline{P F})$ are reciprocal pairs of some involution on pencil of lines pass through $P$.

Proof. Take a pole-polar transformation with respect to $\mathcal{C}$, this is equivalent to Desargues' Involution Theorem. $\square$

又见yau-awards第10页

the corresponding theorem after a duality transformation also holds true: Pascal is the dual of Brianchon, and dDIT is the dual of DIT. For dDIT, we have an involution on the pencil centered at $P$ with reciprocal pairs $P(A C)(B D)(E F)(\omega)$ where $P(\omega)$ denotes two tangents from $P$ to $\omega$.

artofproblemsolving.com/community/c738838h1806500
math.stackexchange.com/questions/4003689/prov … fg-is-tangent-to-abc
mathoverflow.net/questions/70226/how-to-solve … ms-using-involutions

YouTube

• Examples on the Dual of Desargues' Theorem
• LIVESTREAM GEO #87A: Trivialized by the Dual Desargues ...
• LIVESTREAM GEO#92A: Another Problem Trivialized by the Dual Desargues Involution Theorem!

hbghlyj

例题：kuing.cjhb.site/forum.php?mod=viewthread&tid=10542
如图, $OC,OD$ 是 $\angle AOB$ 的一对等角线, $AC$ 与 $BD$ 交于点 $E,$ $AD$ 与 $BC$ 交于点 $F,$ 则 $OE,OF$ 也是 $\angle AOB$ 的一对等角线.

证明：
A,B、C,D、E,F为一个完全四线形的三双对顶点，根据笛沙格对合定理的对偶，存在一个直线对合f，

f(OA)=OB，f(OC)=OD，f(OE)=OF.

“关于角AOB平分线对称”是一个对合g.
由于OA,OB、OC,OD为等角线，g(OA)=OB，g(OC)=OD.
f(OA)=g(OA)、f(OC)=g(OC)这两个条件唯一确定了对合，所以f=g，所以g(OE)=OF，即OE,OF为等角线。

hbghlyj

例题：从 纯几何吧 2371 [专题]等角共轭  28楼2019-02-07 16:45 搬来：

牛顿定理：切四边形的圆锥曲线的中心在该四边形的牛顿线上。

完全四边形ABCDEF，求证：切四边形的圆锥曲线的中心O在牛顿线LMN上。

证明：设P为牛顿线LMN方向的无穷远点，PT₁、PT₂是切四边形的圆锥曲线的切线。
那么直线PA、PB、PC、PD、PE、PF、PT₁、PT₂平行于牛顿线LMN.
因为L是AB中点，所以PA,PB关于LMN对称，同理PC,PD、PE,PF关于LMN对称.
设g是一个对合“关于LMN对称”，则g(PA)=PB，g(PC)=PD，g(PE)=PF.
对P和完全四边形ABCDEF用笛沙格对合定理的对偶，存在一个直线对合f，

f(PA)=PB，f(PC)=PD，f(PE)=PF，f(PT₁)=PT₂.

f(PA)=g(PA)、f(PC)=g(PC)这两个条件唯一确定了对合，所以f=g，所以g(PT₁)=PT₂，所以LMN经过T₁T₂的中点O.

hbghlyj

例题：圆外切四边形 $A B C D$ 的密克点为 $M$，证明∠AMI=∠CMI.

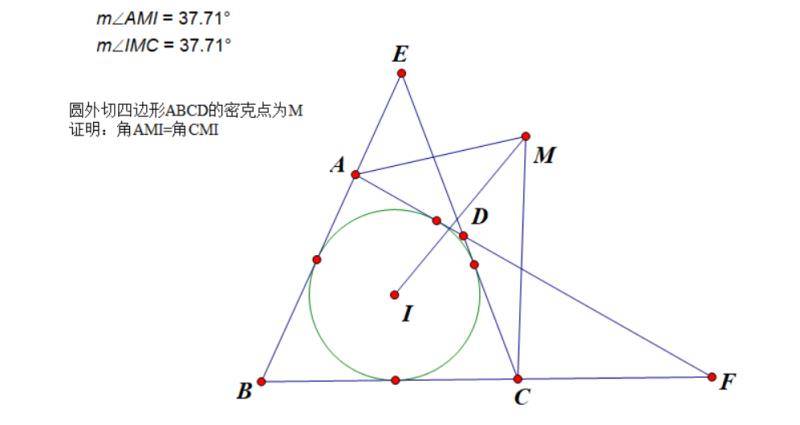
这个用对合怎么证？说明对合的对称轴是MI即可。
作圆的切线MP、MQ.
根据笛沙格对合定理的对偶，存在一个直线对合f，

f(MA)=MC，f(MB)=MD，f(ME)=MF，f(MP)=MQ.

因为M是密克点，有∠AMB=∠DMC.
“关于角AMC平分线对称”是一个对合g，g(MA)=MC，g(MB)=MD.
f(MA)=g(MA)、f(MB)=g(MB)这两个条件唯一确定了对合，所以f=g，
所以g(MP)=MQ，那么对合的对称轴为∠MPQ平分线MI，所以∠AMI=∠CMI.

如果没说M是密克点，只有∠AMB=∠DMC呢？一样地，作出切线，对合依然在。

---

例题：如图, $\triangle A B C$ 的内切圆 $\odot I$ 切 $B C$ 于 $D, D L$ 是 $\odot I$ 的直径, 过 $A$ 作直线交 $\odot I$ 于 $M, N$, 且 $I M \px N L$. 求证: $\angle B M I=\angle I M C$.

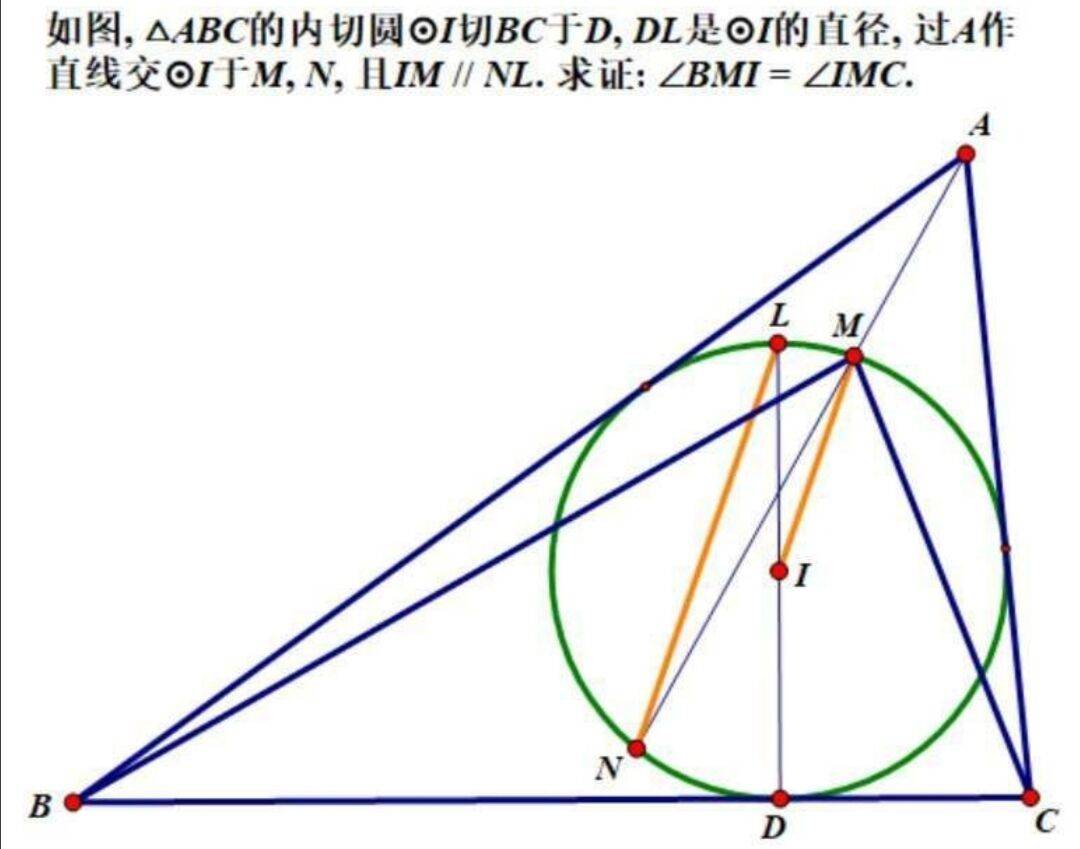
通过平行的条件，导角说明AMD平分线是M处切线，然后把上题的那个M移到这个圆上就好了

hbghlyj

例题：USAMO-2012-notes（PDF｜TeX）第9页 §2.2 USAMO 2012/5
Let $P$ be a point in the plane of $\triangle ABC$,
and $\gamma$ a line through $P$.
Let $A'$, $B'$, $C'$ be the points where the
reflections of lines $PA$, $PB$, $PC$ with respect to $\gamma$
intersect lines $BC$, $CA$, $AB$ respectively.
Prove that $A'$, $B'$, $C'$ are collinear.

Second solution (Desargues involution).
设 $C'' = \overline{A'B'} \cap \overline{AB}$.
对完全四线形 $ABCA'B'C''$ 用笛沙格定理的对偶，存在对合 $\tau$ 交换$(PA,PA')$, $(PB,PB')$, $(PC,PC'')$.
由于$(PA,PA')$, $(PB,PB')$关于 $\gamma$ 对称，这个 $\tau$ 就是关于 $\gamma$ 对称，所以 $C'' = C$.

hbghlyj

例题：Poncelet's Porism artofproblemsolving.com/community/c6h1226573p6939973
设 $\triangle A B C, \triangle D E F$ 内接于圆 $\Gamma$ 且外切于圆 $\omega$.
设 $EF$ 与圆 $\omega$ 切于 $L$，设 $BC$ 与圆 $\omega$ 切于 $K$.
设 $AL$ 交圆 $P$ 于 $N$，设 $DK$ 交圆 $P$ 于 $M$.
证明: $A M, E F, B C, D N$ 共点。

证明：对四边形 $DELF$ 内切圆 $\omega$ 及点 $A$ 用笛沙格对合定理的对偶，
存在对合，交换 $(A D, A L),(A E, A F),(A B, A C)$，
所以存在圆 $\Gamma$ 上的对合，交换 $(B, C),(D, N),(E, F)$，则 $BC, EF, ND$ 共点。
同理 $B C, E F, A M$ 共点。
命题得证。

hbghlyj

Example 3.3 (Taiwan TST3 2014 P3). Let $M$ be any point on the circumcircle of $\triangle A B C$. Suppose the tangents from $M$ to the incircle meet $B C$ at two points $X_1$ and $X_2$. Prove that the circumcircle of $\triangle M X_1 X_2$ intersects the circumcircle of $\triangle A B C$ again at the tangency point of the $A$-mixtilinear incircle.

M是△ABC外接圆上一点，过M作内切圆的两条切线交直线BC于$X_1,X_2$.
$T$是A-伪内切圆切点。证明：$MX_1TX_2$共圆。
证明：设 $M A$ 交 $B C$ 于 $K$.
设内切圆在 $B C$ 上的切点为 $D$.
由这帖知 $∠BTD = ∠CTA$，所以 $AA'\px BC$.
$\because \angle M T A^{\prime}=\angle M A A^{\prime}=\angle K ,\quad \therefore M  D T K$ 共圆.
对四边形 $A B D C$ 及点 $M$ 用笛沙格对合定理的对偶，可知 $(M A, M D),(M B, M C),(M X_1, M X_2)$ 是同一对合的三组对应线，
$\therefore(K, D),(B, C),(X_1,X_2)$ 是同一对合的三组对应点。
$\because P B \cdot P C=P M \cdot P T=P D \cdot P K$
$\therefore P$ 是对合中心（即反演中心）
$\therefore P X_1 \cdot P X_2=P B \cdot P C=P M \cdot P T$
$\therefore M X_1 T X_2$ 共圆。

hbghlyj

intersect on Euler line
artofproblemsolving.com/community/c6h623918p3734836
Let $ABC$ be a triangle with circumcenter $O$. $D,E,F$ are the midpoints of $BC,CA,AB$, respectively. $AO$ cut $(O)$ at $M$, $AD$ cut $(O)$ at $D_1$, $MD$ cut $(O)$ at $D_2$
Similarly, We have $E_1,E_2,F_1,F_2$
Prove that $D_1D_2,E_1E_2,F_1F_2$ intersect on Euler line of triangle $ABC$.