|
|
渝X教师，周伟(2859*****) 21:32:55
这题如何搞
川M教师谨(2758*****) 23:30:46
苏L教师wwdwwd117(2365*****) 0:37:59
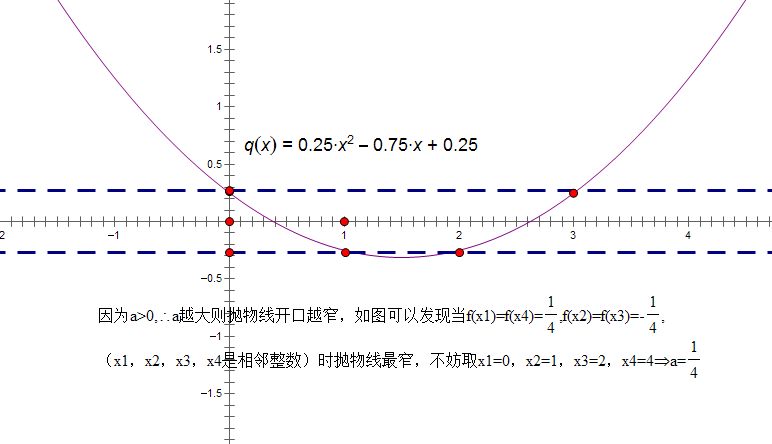
感性解法
这种“感性解法”我觉得不能算是解法，因为太不严谨，顶多算是猜答案，在考场上确实管用。
不过要给出严格的代数解法还真有点难，我当时也没什么好的想法，直到刚才想到拉格朗日插值才勉强搞了出来。
题目：对于函数 $f(x)$，若存在 $x_0\inZ$，满足 $\abs{f(x_0)}\leqslant1/4$，则称 $x_0$ 为函数 $f(x)$ 的一个“近零点”。已知函数 $f(x)=ax^2+bx+c$（$a>0$）有四个不同的“近零点”，则 $a$ 的最大值为
解：依题意可设 $y=f(x)$ 过四点 $(n_1,y_1)$, $(n_2,y_2)$, $(n_3,y_3)$, $(n_4,y_4)$，其中 $n_1<n_2<n_3<n_4$, $n_i\inZ$, $\abs{y_i}\leqslant 1/4$, $i=1$, $2$, $3$, $4$，由拉格朗日插值公式，$f(x)$ 可以写成
\[f(x)=y_1\frac{(x-n_2)(x-n_3)}{(n_1-n_2)(n_1-n_3)}
+y_2\frac{(x-n_1)(x-n_3)}{(n_2-n_1)(n_2-n_3)}
+y_3\frac{(x-n_1)(x-n_2)}{(n_3-n_1)(n_3-n_2)},\]
对比系数得
\[a=\frac{y_1}{(n_1-n_2)(n_1-n_3)}
+\frac{y_2}{(n_2-n_1)(n_2-n_3)}
+\frac{y_3}{(n_3-n_1)(n_3-n_2)},\]
现在，假设 $a>1/4$，则
\[\frac{y_3}{(n_3-n_1)(n_3-n_2)}>\frac14
-\frac{y_1}{(n_1-n_2)(n_1-n_3)}-\frac{y_2}{(n_2-n_1)(n_2-n_3)},\]
于是
\begin{align*}
y_4&=y_1\frac{(n_4-n_2)(n_4-n_3)}{(n_1-n_2)(n_1-n_3)}
+y_2\frac{(n_4-n_1)(n_4-n_3)}{(n_2-n_1)(n_2-n_3)}
+y_3\frac{(n_4-n_1)(n_4-n_2)}{(n_3-n_1)(n_3-n_2)} \\
&>y_1\frac{(n_4-n_2)(n_4-n_3)-(n_4-n_1)(n_4-n_2)}{(n_1-n_2)(n_1-n_3)} \\
&\relph {} +y_2\frac{(n_4-n_1)(n_4-n_3)-(n_4-n_1)(n_4-n_2)}{(n_2-n_1)(n_2-n_3)}
+\frac{(n_4-n_1)(n_4-n_2)}4 \\
&=y_1\frac{n_4-n_2}{n_1-n_2}+y_2\frac{n_4-n_1}{n_2-n_1}
+\frac{(n_4-n_1)(n_4-n_2)}4 \\
&\geqslant -\frac{n_4-n_2}{4(n_2-n_1)}-\frac{n_4-n_1}{4(n_2-n_1)}
+\frac{(n_4-n_1)(n_4-n_2)}4,
\end{align*}
令 $p=n_2-n_1$, $q=n_4-n_2$，则 $p\geqslant 1$, $q\geqslant 2$，代入得
\[y_4>-\frac q{4p}-\frac{p+q}{4p}+\frac{(p+q)q}4
=\frac14+\frac{(p+q)(pq-2)}{4p}\geqslant \frac14,\]
与 $\abs{y_4}\leqslant 1/4$ 矛盾！所以必有$a\leqslant 1/4$。
最后举一例 $f(x)=(x^2-3x+1)/4$ 满足条件，所以 $a$ 的最大值为 $1/4$。 |
|
走走看看
发表于 2017-11-9 16:14
