解析几何与立体几何的完美结合

hjfmhh

第16题求解

kuing

考场解法：
当 MN 无限接近 BC 时，显然交点趋向无穷远，方向与 PQ 平行；
若允许 N 跑到 CD 延长线上，则当 N 无穷远时，交点也跟着无穷远，方向与 RQ 平行。
由此判断出交线为双曲线且两渐近线分别与 PQ、RQ 平行，即两渐近线夹角 60°，可得离心率为 `2/\sqrt3`。

hjfmhh

kuing 发表于 2022-10-8 02:59
考场解法：
当 MN 无限接近 BC 时，显然交点趋向无穷远，方向与 PQ 平行；
若允许 N 跑到 CD 延长线上，则 ...

第二句话方向与RQ平行不好理解

kuing

还是写个正规解法吧……

如下图（左），设 `AN` 交 `QR` 于 `S`，则 `SP` 与 `MN` 相交，设交点为 `T`，则 `T` 就是交线上的点。
设 `QR` 中点为 `U`，由梅氏定理，有
\begin{align*}
-1&=\frac{TP}{PS}\cdot\frac{SA}{AN}\cdot\frac{NM}{MT}\\
&=\frac{TP}{PS}\cdot\frac{-1}2\cdot\frac{BM}{MP}\\
&=\frac{TP}{PS}\cdot\frac{-1}2\cdot\frac{QS}{SU},
\end{align*}
（线段均为有向线段，下同）所以
\[\frac{TP}{PS}=\frac{2US}{SQ},\]

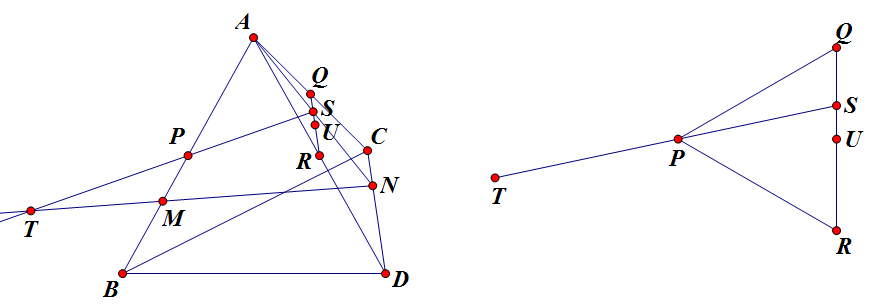
从而转化为平面问题：
如上图（右），正 `\triangle PQR` 中，`U` 为 `QR` 中点，`S` 在 `QR` 上，`T` 在 `PS` 上且满足 `TP/PS=2US/SQ`，求 `T` 的轨迹。

不妨设边长为 `2`，建系使 `P(0,0)`, `U\bigl(\sqrt3,0\bigr)`，设 `S\bigl(\sqrt3,m\bigr)`，则
\[\frac{2US}{SQ}=\frac{2m}{1-m}\riff T\left(-\frac{2m}{1-m}\cdot\sqrt3,-\frac{2m}{1-m}\cdot m\right),\]
消 `m` 即得 `T` 的轨迹方程为
\[y=\frac{x^2}{\sqrt3x-6}=\frac x{\sqrt3}+\frac{12}{\sqrt3x-6}+2,\]
可以看出这是一条平移了的双勾函数，两渐近线分别为 `x=2\sqrt3` 和 `y=x/\sqrt3+2`，与楼上的判断一致。

hjfmhh

kuing 发表于 2022-10-8 15:59
还是写个正规解法吧……

如下图（左），设 `AN` 交 `QR` 于 `S`，则 `SP` 与 `MN` 相交，设交点为 `T`，则 ...

谢谢kuing的精彩解答，二楼我这样理解，但当N在CD延长线上趋于无穷远时，推不出NM与RQ同方向，不知道错在哪里？请高手指教指教

kuing

hjfmhh 发表于 2022-10-10 21:26
谢谢kuing的精彩解答，二楼我这样理解，但当N在CD延长线上趋于无穷远时，推不出NM与RQ同方向，不知道错在 ...

我说的是无穷远的方向，不是说 MN 的方向。