立体几何中的动点问题

lrh2006

如图，等腰直角$\triangle ABC$中，AC=CB，点P为平面ABC外一动点，满足PB=AB=2,
$ \angle PBA $=$ \frac{\pi}{2} $，则存在点P使得（  ）
A.$ AB\perp PC $
B.PB与平面PAC所成角为$\frac{\pi}{4}$
C.PC=$\frac{16}{5}$
D.二面角P-AC-B的大小为$\frac{\pi}{3}$

选项A错误，其他的没看出来，请老师们指教。

我上午发过这个题目的，不知道为什么竟然找不到了，好像没有发出来
第一次用草稿，不要太好用了，不知道是不是用了草稿的缘故，把东西存到别处了，然后我找不到？

kuing

图这样摆会好看一点吧：

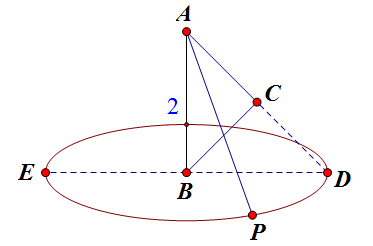
P 的轨迹就是图中的圆（除去 D、E）。

对于 PC 来说显然当 P 在 D 处时最小、在 E 处最大，于是 PC 范围就是 `(\sqrt2,\sqrt{10})`，故 C 错；

对于二面角 P-AC-B 来说显然当 P 趋向 D 时二面角趋向直角、趋向 E 时趋向 0，所以肯定可以取到 60 度，故 D 对。

稍微难看一点的是 B，由于平面 PAC 也就是平面 PAD，注意对称性，可以看出：

BP 与 PAD 所成角 = BD 与 PAD 所成角，

这样就比较易看了，又注意当 P 趋向 D 时这个角趋向 45 度，那么其他的点就只有更小了，所以 45 度是不存在的，B 错。

lrh2006

写得真漂亮，谢谢kk