来自讨论组：两平面垂直，其内有两直线也垂直

kuing

v6mm131 21:50


我想了一下，相比解这道题，以下引理或许更有意义一些。

引理：平面 `\alpha \perp` 平面 `\beta`，直线 `m \subset \alpha`，直线 `n \subset \beta`，且 `m \perp n`，则：`m \perp \beta` 与 `n \perp \alpha` 至少有一个成立。

引理的证明：放在空间直角坐标系中，不妨设 `\alpha`, `\beta` 分别就是平面 `xOz` 和平面 `yOz`，则可设直线 `m`, `n` 的方向向量分别为 `(x_1,0,z_1)`, `(0,y_2,z_2)`，则由 `m\perp n` 得 `0=(x_1,0,z_1)\cdot(0,y_2,z_2)=z_1z_2`，所以 `z_1=0` 或 `z_2=0`，亦即 `m \perp \beta` 或 `n \perp \alpha`。

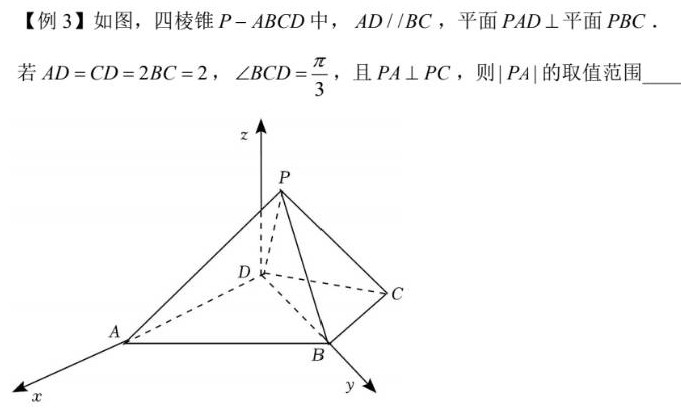
回到原题：由条件易得 `BD\perp BC`，可建系使得 `D(0,0,0)`, `A(2,0,0)`, `B\bigl(0,\sqrt3,0\bigr)`, `C\bigl(-1,\sqrt3,0\bigr)`，设 `P(x,y,z)`。

由条件及引理知 `PA\perp PBC` 或者 `PC\perp PAD`。

若为前者，则 `PA\perp BC`，即 `PA\perp x` 轴，故 `P` 的横坐标 `x=2`，
再作 `PE\perp BC` 于 `E`，则 `E\bigl(2,\sqrt3,0\bigr)`，且 `PA\perp PE`，所以 `P` 的轨迹是以 `AE` 为直径的圆（除 `A`、`E` 外）；

若为后者，同理可得 `P` 的横坐标 `x=-1`，作 `PF\perp AD` 于 `F`，则 `F(-1,0,0)` 且 `PC\perp PF`，所以 `P` 的轨迹是以 `CF` 为直径的圆（除 `C`、`F` 外）。

综上，`P` 的轨迹是两个圆，各挖两对径点。

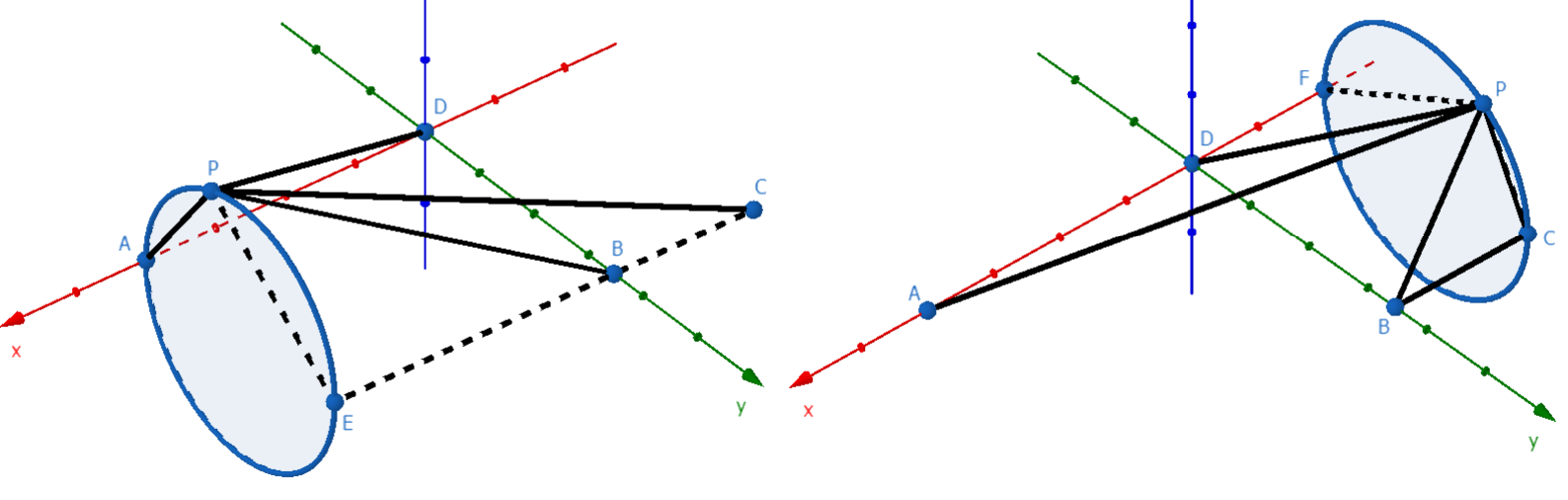
由此易知：
对于第一个圆，`PA` 的范围为 `(0,AE)`，即 `\bigl(0,\sqrt3\bigr)`；
对于第二个圆，`PA` 的范围为 `(AF,AC)`，即 `\bigl(3,2\sqrt3\bigr)`。
所以答案为 `\bigl(0,\sqrt3\bigr)\cup\bigl(3,2\sqrt3\bigr)`。