|
|
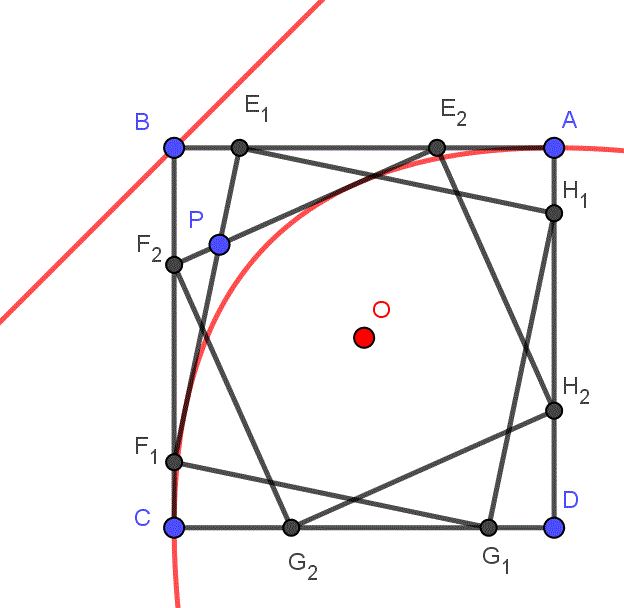
Last edited by hbghlyj 2023-9-8 12:28| 单位正方形ABCD的中心为O,过O作AB,BC的平行线与AB,BC形成一个正方形区域,点P在该区域内,求作正方形EFGH内接于ABCD,其中E,F分别在AB,BC上,使得线段EF经过点P. |
|
引理:正方形EFGH内接于ABCD,则EF的包络是以O为焦点,过B作的BD垂线为准线的抛物线.
证明
设P到BC,AB的距离为a,b,则当且仅当$(a-b)^2- 2a - 2b \ge -1$时问题有解.取等时P在抛物线上,所以只有一解.取严格小于时有两解.
设BE=x, 则BF=1-x,$\dfrac ax+\dfrac b{1-x}=1\Rightarrow x^2+(b-a-1)x+a=0$
所以该问题是尺规可作的。
能否从几何性质得出简单的尺规作法呢? |
|