|
|
original poster
isee
posted 2023-1-11 21:46
Last edited by isee 2023-1-11 22:34如果 乌贼 路过可以鉴定下.
这里直接三角法,不作辅助线.
记$B=4\alpha$,$A=90^\circ-\alpha$,则由正弦定理有\[\frac{15}{27}=\frac{\sin (A+4\alpha)}{\sin A}=\frac{\cos 3\alpha}{\cos\alpha},\]
由三倍角公式 $\cos3\alpha=4\cos^3\alpha-3\cos\alpha$ 得到\[\frac{15}{27}=4\cos^2\alpha-3,\Rightarrow \cos \alpha=\frac{2\sqrt 2}3,\,\cos 3\alpha=\frac{30\sqrt 2}{81}.\]
从而 \[\cos A=\sin \alpha=\frac13,\,\cos C=-\cos(A+4\alpha)=\sin3\alpha=\frac{23}{27}.\]
再由第一余弦定理 $c=c\cos A+a\cos C$,有\[AC=15\cos A+27\cos C=5+23=28.\]
哦,数字这么整~
那看看四等分角 B,如图 2,转化为知角 B 的平分线长 AA'=15,求 AC.
这确实是一道初中题了(张角定理,斯特瓦尔特定理等均可以求了)
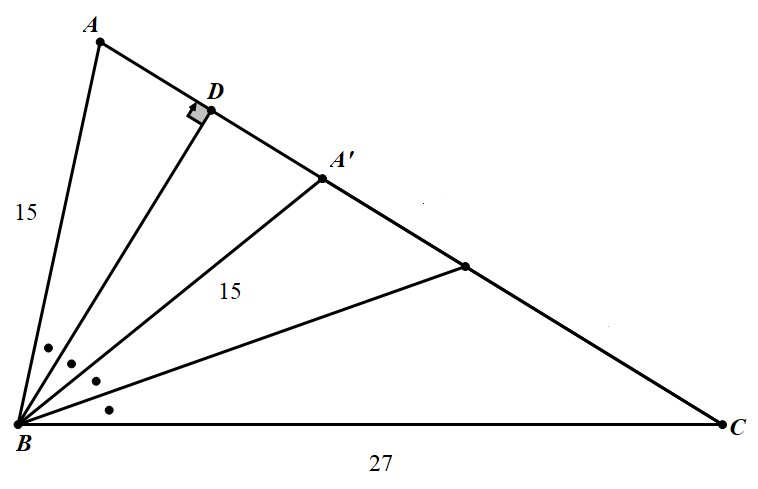
图 2
|
|