|
|
Author |
hbghlyj
Posted at 2024-12-29 05:48:48
《Geometry in figures》问题 2.37.
问题 2.37. 设 $A B C D E$ 是一个凸五边形，$A C \cap B E=D'$, $B D \cap A C=E'$, $B D \cap E C=A'$, $E C \cap A D=B'$, $A D \cap B E=C'$. 设 $(X Y Z)$ 表示 $\triangle X Y Z$ 的外接圆。
设 $(A D' B) \cap (B E' C)=\{B, B''\}$
设 $(B E' C) \cap(C A' D)=\{C, C''\}$
设 $(C A' D) \cap (D B' E)=\{D, D''\}$
设 $(D B' E) \cap(A C' E)=\{E, E''\}$
设 $(A C' E) \cap (A D' B)=\{A, A''\}$
证明：直线 $A A'', B B'', C C'', D D''$ 和 $E E''$ 是共点的。
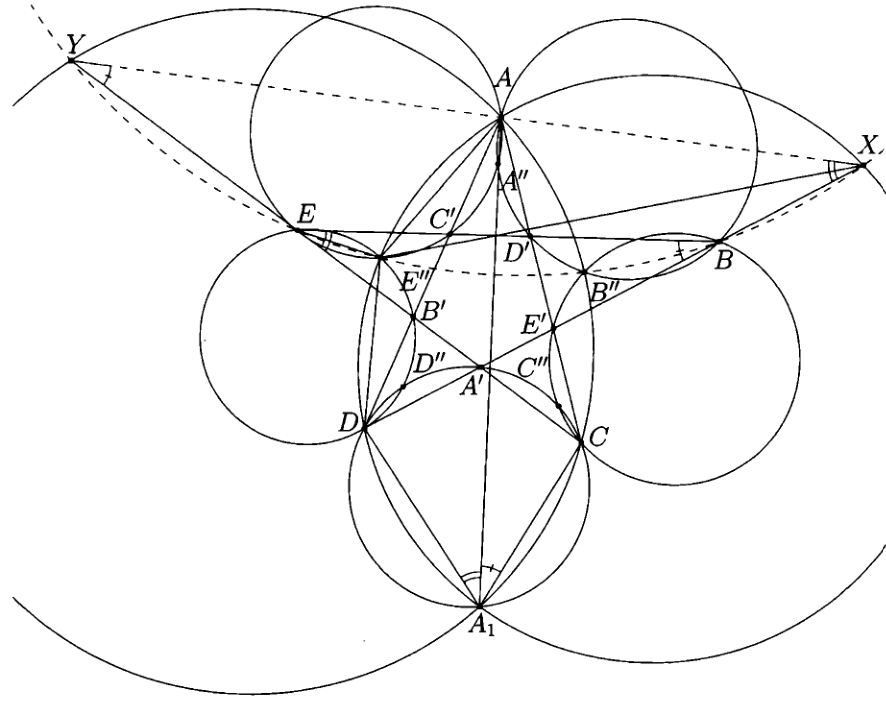证明：根据根轴定理，只需证明四边形 $B B'' E'' E$ 是圆内接的。设 $(A D E'') \cap(A C B'')=A_{1}$。
我们有
\begin{align*}
\angle B E C &=180^{\circ}-\angle E B' C'-\angle E C' B'=\angle E C' A+\angle E B' D-180^{\circ} \\
&=\angle A E'' E+\angle D E'' E-180^{\circ}=180^{\circ}-\angle A E'' D=\angle A A_{1} D
\end{align*}
类似地，我们得到 $\angle E B D=\angle A A_{1} C$。但是
$$
\angle B A' C=\angle E B D+\angle B E C=\angle D A_1 C .
$$
因此，四边形 $D A_{1} C A'$ 是圆内接的。设 $D B \cap(A D E'')= \{D, X\}$ 并且设 $C E \cap(C B'' A)=\{C, Y\}$。现在我们有
$$
\angle X A Y=\angle X A A_{1}+\angle Y A A_{1}=\angle X D A_{1}+\angle Y C A_{1}=180^{\circ}
$$
因此，点 $X, A$ 和 $Y$ 是共线的。因此，$\angle X Y E= \angle A A_{1} C=\angle E B A'$，所以四边形 $X Y E B$ 是圆内接的。此外，
$\angle X E'' E=\angle X E'' A+\angle A E'' E=\angle X D A+\angle B C' D=180^{\circ}-\angle E B D=\angle X B E$。
因此，四边形 $X B E'' E$ 是圆内接的，类似地，四边形 $Y E B'' B$ 也是圆内接的，但四边形 $X Y E B$ 也是圆内接的。由此可见，六边形 $X Y E E'' B'' B$ 是圆内接的。
|
|
给定平面内的五个点 A1, ..., A5，按上述构造的五个根轴
g1, ..., g5 共点或平行。