三倍角公式 级数

hbghlyj

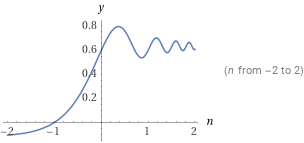
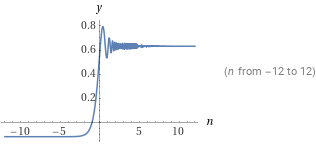
$$ \sum_{k=0}^\infty \frac{\sin^3(3^k)}{3^k} =\frac{3\sin(1)}4$$
部分和：
$$ S(n) = \sum_{k=0}^n \frac{\sin^3(3^k)}{3^k} = \frac{3\sin(1)-3^{-n}\sin(3^{n+1})}{4}  $$
证明：由公式$ \sin(3a) = 3 \sin(a) - 4 \sin^3(a) $得
$$ \sin^3(a)=\frac{3 \sin(a)- \sin(3a)}4 .$$  
代入$a=3^k$:
\begin{eqnarray*}
  S(n) &=& \sum_{k=0}^n \sin^3(3^k)/3^k  \\
       &=& \frac14\sum_{k=0}^n [3 \sin(3^k)-\sin(3^{k+1})]/3^k  \\
       &=& \frac{3}{4}[\sum_{k=0}^n \sin(3^k)/3^k-\sum_{k=0}^n \sin(3^{k+1})/3^{k+1}]\\&=&\frac{3\sin(1)-3^{-n}\sin(3^{n+1})}{4}
\end{eqnarray*}