二元多项式有2个极大值点而没有其他驻点，有低于6次的例子吗

hbghlyj

二元多项式在$\mathbb{R}^2$可能有两个极大值点而没有其他驻点。

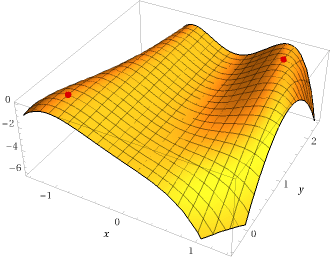
例子：Counting Critical Points of Real Polynomials in Two Variables第7页 $$f(x,y)=-(x^2-1)^2-(x^2y-x-1)^2$$在 $(-1,0)$ 和 $(1,2)$ 处有两个极大值而没有其他驻点。WolframAlpha ResourceFunction["StationaryPoints"][-(x^2-1)^2-(x^2y-x-1)^2,{x,y}]
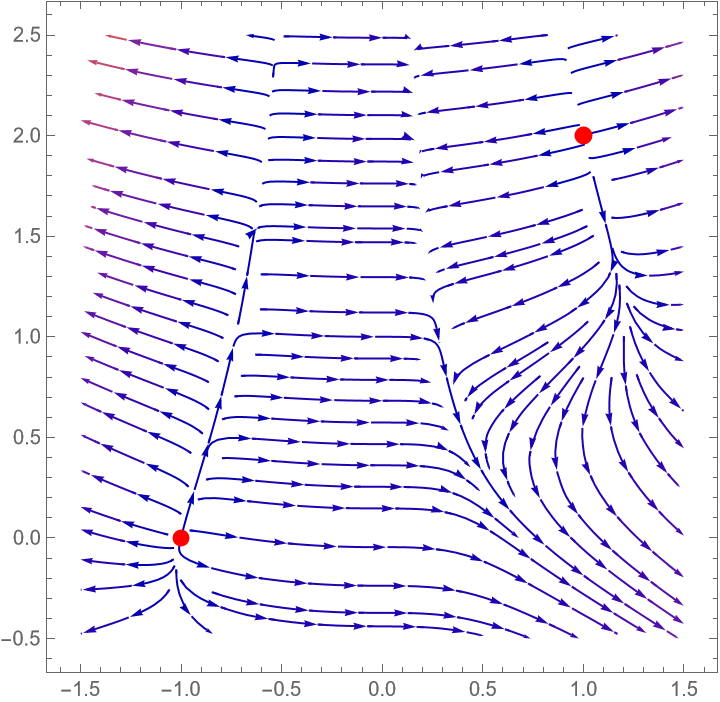
Show[StreamPlot[Evaluate[-Grad[-(x^2-1)^2-(x^2 y-x-1)^2,{x,y}]],{x,-1.5,1.5},{y,-0.5,2.5},MaxRecursion->5],Graphics[{Red,PointSize[0.025],Point[{-1,0}],Point[{1,2}]}]]

问题：有低于6次的例子吗？

hbghlyj

前帖的4次例子$\left[\left(x-\frac{1}{3}\right)^2+\left(y-\frac{2}{3}\right)^2\right]\cdot\left[\left(x-\frac{2}{3}\right)^2+\left(y-\frac{1}{3}\right)^2\right]$有一个鞍点$(\frac12,\frac12)$不符合条件。

对称多项式都不符合条件吗？

hbghlyj

相关：math.stackexchange.com/questions/4024737/if-a … l-it-necessarily-hav