请教：四面角四角相等

数学小黄

设P，A，B，C和D是空间中不同的五个点，使得∠APB=∠ BPC=∠CPD=∠DPA=Θ，这里Θ是一个给定的锐角。试确定∠APC+∠BPD的最大值和最小值。

joatbmon

可以看到，所求两个角$\angle APC=\angle BPD$
这显然与AP,BP,CP,DP的长度无关，那么都取1，就是一个正四棱锥，$\cos\angle APC=1-4(\cos\theta-1)^2$
好奇怪，我哪里理解错了？

kuing

回复 2# joatbmon

显然可以不相等，想想菱形……

To 楼主：下次发贴时可以选择主题分类（见 kuing.cjhb.site/forum.php?mod=viewthread&tid=170），标题也可以打详细一些。

kuing

作公共平分线，再作一与此线垂直的平面，如图。



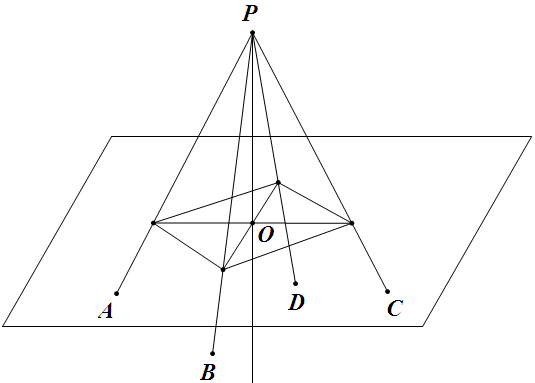
记 $\angle APO=\alpha$, $\angle BPO=\beta$，则由三余弦定理得
\[\cos\theta=\cos\alpha\cos\beta=\frac12\bigl( \cos(\alpha-\beta)+\cos(\alpha+\beta)\bigr),\]
即
\[\cos\frac{\angle APC+\angle BPD}2=2\cos\theta-\cos(\alpha-\beta),\]
显然 $\abs{\alpha-\beta}\in[0,\theta]$，故
\[\cos\frac{\angle APC+\angle BPD}2\in[2\cos\theta-1,\cos\theta],\]
即
\[\angle APC+\angle BPD\in[2\theta,2\arccos(2\cos\theta-1)].\]

数学小黄

回复 4# kuing


    管理员厉害！！！

hbghlyj

这个问题甚至出现在网络小说中
mkehuan.bookresource.qq.com/chapter/1035403727/733859881/
　　以后你们要是有什么数学方面的问题，还是晚上在林老师那边问我好一些。” 　　反正赵贤才晚上在教室上晚自习是做题，去了林老师那边，除了给他们讲题之外，也是做题。 　　在哪做题不是做？ 　　既然如此，那还不如晚上去林老师的数竞辅导课那边呢。 　　季兴磊他们一听赵贤才这么说，也是对赵贤才连连称谢，之后很快便离开了高二七班的教室。 　　“没想到你现在在高三那边名气也这么大了。” 　　“他们来问的是什么题目？我看看。” 　　“他们问的肯定都是些数学竞赛的题目，你能看懂啥呀。” 　　…… 　　季兴磊他们这几个非本班的学生跑来七班，自然会吸引七班同学们的注意。 　　更何况他们来找的还是赵贤才，就更引人注意了。 　　等他们走后，围在赵贤才这边的同学们便开始议论起来。 　　而赵贤才桌上的那张写了几道数学竞赛难题的草稿纸，此时也在程志均的手里，看得起劲的还有周以直和王一松这两位。 　　“第一题，设P，A，B，C和D是空间中不同的五个点，使得∠APB=∠ BPC=∠CPD=∠DPA=Θ，这里Θ是一个给定的锐角。 　　试确定∠APC+∠BPD的最大值和最小值。 　　第二题，试找出不能表示为(2^a-2^b)/(2^c-2^d)的形式的最小正整数，其中a、b、c、d都是正整数。 　　第三题，求最大自然数x，使得对每一个自然数y，x能……” 　　“啥啥啥，这都写的啥？” 　　“算了，算了，我不看了，你们谁爱看谁看去吧。” 　　看完季兴磊他们交给赵贤才那张草稿纸上写的几道数学题后，程志均便将这张草稿纸还给了赵贤才，他们几个也是都放弃了再研究下去的想法。