求证一个组合恒等式

TSC999

$\binom{2 n+1}{n+1}=1+\sum_{k=1}^n \binom{n+k}{n}$

kuing

这两天玩惯了“最短路径”，恰好这里也可以用上。



在方形网格中，由 $(0,0)$ 到 $(n,n+1)$ 的最短路径总数为 $C_{2n+1}^{n+1}$，
在这当中，如图所示，
路径经过线段 $l_0$ 的共有 $C_{2n}^n$ 条，
经过线段 $l_1$ 的共有 $C_{2n-1}^n$ 条，
经过线段 $l_2$ 的共有 $C_{2n-2}^n$ 条，
……，
经过线段 $l_n$ 的只有 $1$ 条，
全部加起来就是你要证的等式。

TSC999

谢谢 kuing 大师的精彩解答。
我也很赞成您的口号：珍爱生命，远离考试。
善于研究的人不一定善于考试，善于考试的人不一定善于研究。而没有研究能力的人即使学历很高，也难有大的作为。

kuing

干脆写个推广式吧，用同样的方法。

设 $n\inN^+$, $r$, $s\inN$，在方形网络中，由 $(0,0)$ 到 $(n,r+s+1)$ 的最短路径总数为 $C_{n+r+s+1}^{r+s+1}$。



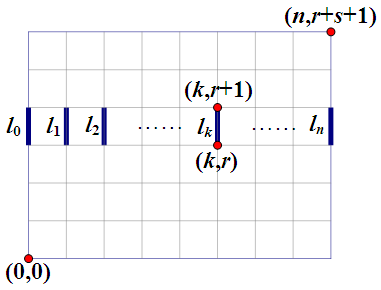
现在，设线段 $l_k$（$k=0$, $1$, \ldots, $n$）的两端点坐标分别为 $(k,r)$, $(k,r+1)$，如图所示，考虑那些最短路径中经过线段 $l_k$ 的条数，因为由 $(0,0)$ 到 $(k,r)$ 的最短路径有 $C_{k+r}^r$ 条，由 $(k,r+1)$ 到 $(n,r+s+1)$ 的最短路径有 $C_{n-k+s}^s$ 条，两者的乘积就是经过 $l_k$ 的条数，所以我们得到恒等式
\[
C_{n+r+s+1}^{r+s+1}=
\sum_{k=0}^nC_{k+r}^rC_{n-k+s}^s,
\]
具体写出来就是
\[
C_{n+r+s+1}^{r+s+1}=
C_r^rC_{n+s}^s+C_{1+r}^rC_{n-1+s}^s+C_{2+r}^rC_{n-2+s}^s+\cdots
+C_{n-1+r}^rC_{1+s}^s+C_{n+r}^rC_s^s,
\]
当 $r=0$, $s=n$ 时就是楼主的等式。