|
|
Last edited by isee at 2022-12-10 00:27:00源自知乎提问
原问题中的直线 " $y=\pm b/a$ " 改为" $y=\pm b\color{red}x/a$ "来写.
题：过双曲线 $x^2/a^2-y^2/b=1$ 左顶点 $A_1P$ 的弦交两渐近线从左至右分别为B，C，若 C 为 BP 中点，且 $\angle A_1PA_2=\pi/4$ ，如图 1，则双曲线的离心率为______.
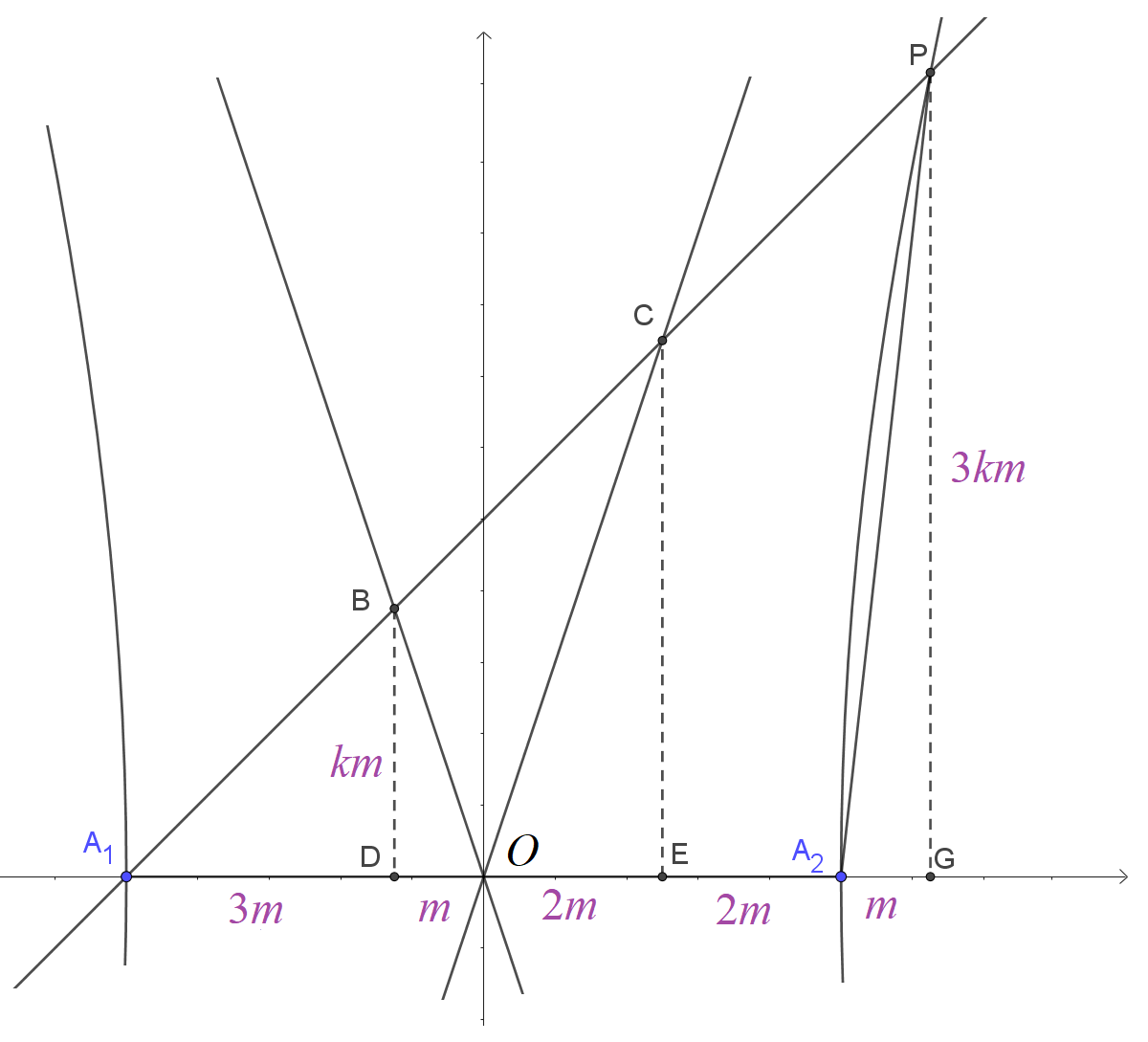
图 1
设 $\color{blue}{b/a=k}$，$\color{blue}{DO=m}$ ，
在双曲线中有经典结论：“直线被双曲线及其渐近线所截得的对应线段相等”，本坛证明1，证明2
如图 1 即有 $A_1B=CP(=BC)$，设 B，C，P 三点在 x 轴上的射影分别为 D，E，G，
则 $A_1D=DE=EG,$ 则由与两渐近线相交可知 $\triangle BDO\sim\triangle CEO$ ，相似比 $\frac{BD}{EC}=\frac{A_1B}{AC}=\frac 12$，
则 $OE=2m$ , $A_1D=DE=DO+OE=3m=EG$， $OA_1=OA_2=4m.$
进一步在 $\triangle BCO$ 中 $BD=k\cdot DO=km,$ 于是 $PG=3BD=3km.$
总之，（不难求得）各线段数量如图 1 所标记.
从而 \[\tan PA_1A_2=\frac {km}{3m}=\frac k3,\; \tan PA_2G=\frac{3km}{m}=3k.\] 在 $\triangle PA_1A_2$ 中，由外角定理知 \[3k=\tan PA_2G=\tan \big(PA_1A_2+45^\circ\big)=\frac{k/3+1}{1-k/3},\] 解得 \[\frac ba=k=\frac {4\pm\sqrt 7}3\Rightarrow e=\sqrt{1+(b/a)^2}=\frac{2(\sqrt 7\pm 1)}3.\] |
|
色k
Posted at 2022-12-10 00:12:51
