$ℝ$上函数$f$在$0$的任何邻域内无界;当$x→0$,$f$不趋于$∞$

hbghlyj

汪林《实分析中的反例》高等教育出版社 (2014) Page 20
11.函数$f$在$0$的任何邻域内都是无界的,但当$x→0$时$f(x)$并不趋于$\infty$.
设 $f(x)=\left|\frac{\cos \frac{1}{x}}{x}\right|$, 则对无论多大的正数 $M$, 总有充分接近于 $x=0$ 的点, 使
$$
\left|\frac{\cos \frac{1}{x}}{x}\right|>M
$$
例如, 取 $x=1 /(n \pi)$, 则 $|\cos (1 / x) / x|=n \pi$, 故当 $n>M / \pi$ 时, 就有
$$
\left|\frac{\cos \frac{1}{x}}{x}\right|>M
$$
即函数 $f$ 在 $x=0$ 的任何邻域内都是无界的.
取 $x_n=\frac1{\left(n+\frac{1}{2}\right) \pi}$, $\cos \frac{1}{x_n}=0$. 当 $n \rightarrow \infty$ 时 $x_n \rightarrow 0$, ${\cos \frac{1}{x_n} \over x_n} \rightarrow 0$, 即当 $x \rightarrow 0$ 时, $\lim f(x)$ 不存在.
注 无界函数的定义与函数趋于无穷大的定义有些相似: 若 $x \rightarrow x_0$ 时, $f(x) \rightarrow \infty$, 则 $f$ 在 $x_0$ 的每个邻域内必定无界. 但是, 这个命题之逆并不成立.
WolframAlpha plot:
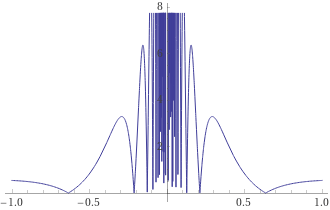
在x∈[0.5,1]的弧长为1.52552 WolframAlpha
评论
$f$在$0$的任何邻域内无界 等价于: 存在数列$\an$满足$\lim|f(a_n)|=\infty$
当$x→0$时$f(x)\to\infty$ 等价于: 对每个趋于$0$的数列$\an$都成立$\lim|f(a_n)|=\infty$

hbghlyj

与上例类似。考虑$(0,1)$上的函数$f(x)=1/x + \cos(1/x)$，显然$\lim_{x→0+} f(x)=+∞$。
$f'(x)={\sin(1/x)-1\over x^2}$，若令$x=1/(2n+1/2)π$，当$n→∞$时$f'(x)=0$，这说明$f'(x)→∞$是不成立的。