|
|
源自知乎提问.
题:若 $\theta\in\left(0,2\pi\right)$,则 $\displaystyle f(\theta)=\frac{\sqrt{3}\sin \theta+\cos \theta+2}{\sqrt{5+4\cos \theta}}$ 的最大值为_______.
见题第一感觉似乎可以转化为点到直线的距离 \[f(\theta)=\frac{\sqrt{3}\sin \theta+\cos \theta+2}{\sqrt{5+4\cos \theta}}=\frac{\sqrt 3\sin\theta+1\cdot (2+\cos\theta)}{\sqrt{\sin^2\theta+(2+\cos\theta)^2}},\] 这样便是点 $A(\sqrt 3,1)$ 到过原点的直线 $l:x\sin\theta+y(2+\cos\theta)=0$ 的最大值,最理想便是 $\sqrt{(\sqrt3-0)^2+(1-0)^2}=2$ ,取等条件是直线 $l$ 的斜率为 $-\sqrt 3$ ,但是取不到,这是因为,容易求得直线 $l$ 的斜率为\[k=-\frac{\sin\theta}{2+\cos\theta}\in [-\sqrt 3/3,\sqrt 3/3].\] 而 $-\sqrt 3\notin [-\sqrt 3/3,\sqrt 3/3]$ .
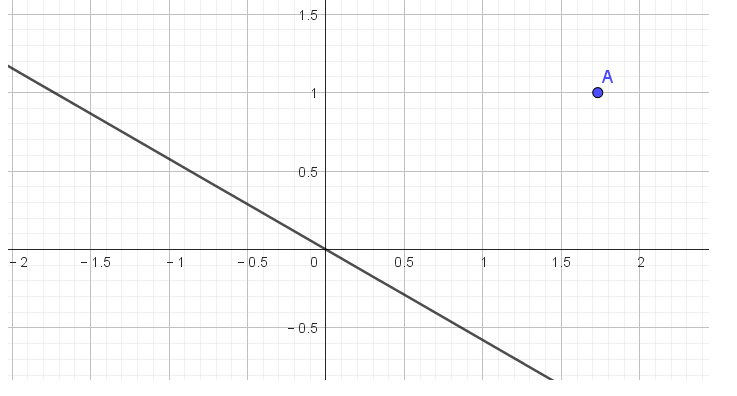
图 1 点 A在直线 l 上方
亦即需调整,如图 1 当 $k_{\min}=-\frac1{\sqrt 3}$ 时,点 $A(\sqrt 3,1)$ 到直线 $x+\sqrt 3y=0$ 的距离达到最大 $\frac{|\sqrt 3+\sqrt 3|}{\sqrt4}=\sqrt 3$ ,也就是 $f(\theta)\leqslant\sqrt 3,$ 此时 $-\frac{\sin\theta}{2+\cos\theta}=-\frac1{\sqrt 3}$. |
|