|
|
Author |
hbghlyj
Posted at 2023-7-26 04:34:33
Last edited by hbghlyj at 2023-7-26 06:34:00
圆环\begin{equation}\label{torus}(\sqrt{x^2+y^2}-2)^2+z^2=1\end{equation}(关于$y$轴旋转45°)作代换$(x, y, z)⟶\left({x + z\over\sqrt2}, y, {z - x\over\sqrt2}\right)$得\begin{equation}\left(\sqrt{\left(x + z\over\sqrt2\right)^2+y^2}-2\right)^2+\left(z - x\over\sqrt2\right)^2=1\label{transformed torus}\end{equation}
令LHS关于$z$的偏导等于$0$得$$\frac{{\left(x + z\right)} {\left(\sqrt{\frac{1}{2} \, {\left(x + z\right)}^{2} + y^{2}} - 2\right)}}{\sqrt{\frac{1}{2} \, {\left(x + z\right)}^{2} + y^{2}}} - x + z=0$$
即
\begin{equation}\label{profile}
\frac{x+z}z=\sqrt{\frac{1}{2} \, (x+z)^{2} + y^{2} }
\end{equation}
从\eqref{transformed torus}与\eqref{profile}消去$z$得
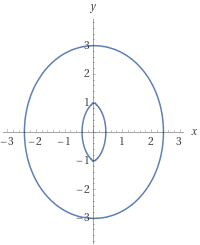
WolframAlpha\begin{equation}\label{result}4 x^8 + 12 x^6 (y^2 - 1) + x^4 (13 y^4 - 62 y^2 - 59) + 6 x^2 (y^2 - 7) (y^2 - 1)^2 + (y^2 - 9) (y^2 - 1)^3 = 0\end{equation}
|
|
kuing
Posted at 2023-7-25 13:58:32
