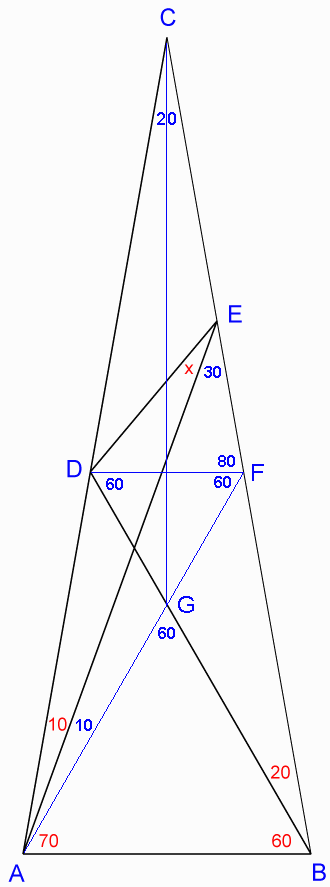
|
|
Solution
1. Calculate some known angles:
\[\angle ACB = 180-(10+70)-(60+20) = 20^{°}\]
\[ \angle AEB = 180-70-(60+20) = 30^{°} \]
2. Draw a line from point $D$ parallel to $AB$, labeling the intersection with BC as a new point $F$ and conclude:
\[ \triangle DCF\sim \triangle ACB \]
\[\angle CFD = \angle CBA = 60+20 = 80^{\circ} \]
\[ \angle DFB = 180-80 = 100^{\circ} \]
\[ \angle CDF = \angle CAB = 70+10 = 80^{\circ}\]
\[ \angle ADF = 180-80 = 100^{\circ}\]
\[ \angle BDF = 180-100-20 = 60^{\circ} \]
3. Draw a line $FA$ labeling the intersection with $DB$ as a new point $G$ and conclude:
\[ \triangle ADF \cong \triangle BFD\]
\[ \angle AFD =\angle BDF = 60^{\circ}\]
\[ \angle DGF = 180-60-60 = 60^{\circ} =\angle AGB\]
\[ \angle GAB = 180-60-60 = 60^{\circ}\]
$ \triangle DFG $(with all angles $60^{\circ})$ is equilateral
$ \triangle AGB$ (with all angles $60^{\circ})$ is equilateral
4. $\triangle CFA$ with two $20^{\circ}$ angles is isosceles, so $FC = FA$
5. Draw a line $CG$, which bisects $\angle ACB$ and conclude:
\[\triangle ACG \cong \triangle CAE\]
\[ FC-CE = FA-AG = FE = FG\]
\[ FG = FD, \text{so}\qquad FE = FD\]
6. With two equal sides, DFE is isosceles and conclude:
\[ \angle DEF = 30^{\circ}+x = (180-80)/2 = 50^{\circ}\]
\[ x=20^{\circ}\]
 |
|
kuing
posted 2013-9-22 14:46
pxchg1200
posted 2013-9-22 14:57
