初中几何角度计算

wzyl1860

题目：在三角形`ABC`中，点`E`在三角形内部满足`\angle ABE=14^\circ`，`\angle EBC=8^\circ`，`\angle EAC=38^\circ`，`\angle EAB=68^\circ`，求`\angle ECB`的度数。

isee

设`\angle ECB=x`，则由Ceva定理角元形式得\[\frac {\sin 14^\circ}{\sin 8^\circ}\cdot\frac {\sin x}{\sin (52^\circ-x)}\cdot\frac {\sin 38^\circ}{\sin 68^\circ}=1.\]
去分母化，积化和差得
\[\sin x(\cos 52^\circ-\cos (-24^\circ))=\sin(52^\circ-x)(\cos 76^\circ-\cos (-60^\circ)),\]
即
\[\sin x\cos 52^\circ-\sin x\cos 24^\circ=\sin(52^\circ-x)\cos 76^\circ-\sin(52^\circ-x)\cos 60^\circ\]
再次积化和差得
\[\sin (x+52^\circ)+\sin (x-52^\circ)-\sin (x+24^\circ)-\sin (x-24^\circ)=\sin(128^\circ-x)+\sin(-24^\circ-x)-\sin(112^\circ-x)-\sin(-8^\circ-x),\]
合并左右两边相等的项，并化简
\[\sin (x-52^\circ)-\sin (x-24^\circ)=-\sin(68^\circ+x)+\sin(x+8^\circ),\]
即
\[\sin (x-52^\circ)+\sin(68^\circ+x)=\sin (x-24^\circ)+\sin(x+8^\circ),\]
两边和差化积得
\[\sin(x+8^\circ)\cos(-60^\circ)=\sin(x-8^\circ)\cos(-16^\circ),\]
整理为
\[f(x)=\frac {\sin(x+8^\circ)}{\sin(x-8^\circ)}=2\cos16^\circ,\]
求导函数`f(x),0^\circ<x<52^\circ`易得`f(x)`是减函数，而`f(24^\circ)=2\cos 16^\circ`，于是`\angle ECB=24^\circ`.



当然，这解法肯定不合楼主要求，写就发上来参考一下，楼下继续~~

kuing

回复 3# isee

忽然想到一个非常简单的三角法，从正切入手。

不妨设 `AD=1`，则易知 `CD=\tan38\du`, `DE=\tan68\du\tan8\du`，故
\[\tan\angle ECD=\frac{\tan68\du\tan8\du}{\tan38\du}=\tan68\du\tan8\du\tan52\du,\]注意右边三个角度恰好为 `8\du`, `60\du+8\du`, `60\du-8\du`，故由三倍角公式，上式即 `\tan\angle ECD=\tan(3\times8\du)`。

isee

回复 4# kuing


    垂直还是有用

乌贼

如图：
点$ C $关于$ AD $的对称点为$ C_1 $，$ AC_1 $延长线交$ AB $垂直平分线$ MN $于$ N $。有$ BC_1 $为$ \angle FBN $的角平分线，$ NC_1 $为$ \angle BNF $的外角平分线，故$ FC_1 $为$ \angle NFE $的平分线，即\[ \angle C_1FE =38\du =\angle C_1AE \]所以$ AEC_1F $四点共圆，得\[ \angle AC_1E=\angle AFE=28\du \\\angle ECD=\angle EC_1D=24\du  \]

乌贼

哈哈，可以用上这一结论   
forum.php?mod=viewthread&tid=5980&highlight=
如图：
$ DA $交$ \triangle ABC_1 $外接圆于$ F $由结论知\[ \angle DEC_1=3\angle DFC_1=66\du  \]

isee

    垂直还是有用


isee 发表于 2021-7-30 18:58

仿4#又解决一个类似的

题：点 $P$ 为 $\triangle ABC$ 内一点满足 $\angle PAB=20^\circ,$ $\angle PAC=10^\circ,$ $\angle PBA=40^\circ,$ $\angle PBC=30^\circ,$求 $\angle ACP.$





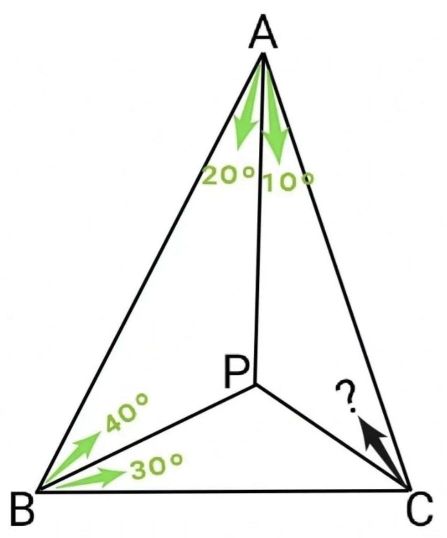
注意到 $AP\perp BC$ 的，故延长 $AP$ 交 $BC$ 于 $Q,$ 不妨设高 $AQ=1.$

则在 Rt$\triangle AQC$ 中， $CQ=\tan 10^\circ,$ 同理 $BQ=\tan 20^\circ,$ 于是在 Rt$\triangle BPQ$ 中， $PQ=\tan 20^\circ\tan 30^\circ,$ 从而在 Rt$\triangle CPQ$ 中

$$\bm{\tan PCQ=\frac {\tan 20^\circ\tan 30^\circ}{\tan 10^\circ}=\tan 20^\circ\tan 30^\circ\tan 80^\circ},$$

由正切三倍角公式有

\begin{align*} \tan \color{blue}3\times \color{blue}{20^\circ}&=\tan 20^\circ\tan (60+\color{blue}{20^\circ})\tan (60-\color{blue}{20^\circ})\\[1em] \iff \tan 20^\circ\tan 80^\circ&=\frac{\tan 60^\circ}{\tan40^\circ}, \end{align*}

从而 $$\tan PCQ=\tan 20^\circ\tan 30^\circ\tan 80^\circ=\frac{\tan 30^\circ\tan 60^\circ}{\tan40^\circ}=\tan 50^\circ,$$

这表明 $\angle PCB=50^\circ\ \iff  \ \angle ACP=30^\circ.$