与圆相切的线段的中点轨迹是双曲线的推导过程

郝酒

中点轨迹是双曲线，顶点是圆和x轴的交点。

有没有直接通过几何的论证方法啊？

郝酒

经网友提示，给出一个中点弦的论证，不知纯几何的方法。
设$M(x_0,y_0)$，所以$k_{AB}=\frac{k^2x_0}{y_0}$
直线AB的方程：
$$y=k_{AB}(x-x_0)+y_0$$
与圆$(x-a)^2+y^2=\frac{a^2k^2}{1+k^2}$相切，所以
$$\frac{\left|k_{AB}a+y_0-k_{AB}x_0\right|}{\sqrt{1+k_{AB}^2}}=\frac{ak}{\sqrt{1+k^2}}$$
化简之后为
$$k^2x^2-2ak^2x+\frac{a^2k^2}{1+k^2}-y^2=0$$
即
$$k^2(x-a)^2-y^2=\frac{a^2k^4}{1+k^2}$$
顶点为$\left(a\pm\frac{ak}{\sqrt{1+k^2}},0\right)$，渐近线斜率$\pm k$，焦点$(a\pm ak,0)$.

游客

圆心就是对称中心，顶点就是圆与X轴的交点，渐近线与已知两直线平行，这些都可以从图中看出，就是焦点位置用几何图形不好找。

kuing

依照观察出来的渐近线的特点，勉强搞出了个这样的几何解法：

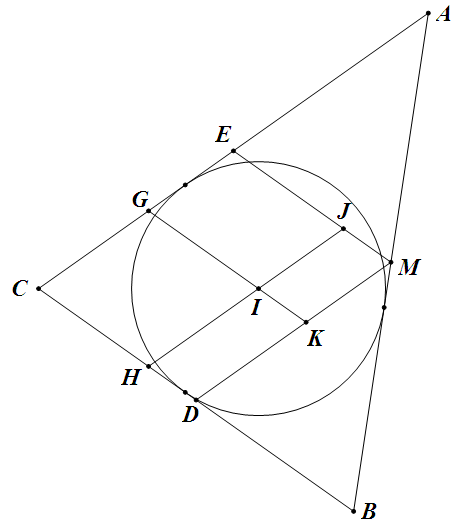
取另外两边的中点 $D$, $E$，过 $I$ 作两边平行线构成如图所示，由海伦公式有
\[r=\frac{2S}{a+b+c}=\frac{\sqrt{(a+b-c)(b+c-a)(c+a-b)}}{2\sqrt{a+b+c}},\]
设菱形 $CGIH$ 的边长为 $m$，易见
\[m=\frac r{\sin C}=\frac{2S}{(a+b+c)\sin C}=\frac{ab}{a+b+c},\]
于是
\begin{align*}
MJ\cdot MK&=\left( \frac a2-m \right)\left( \frac b2-m \right) \\
&=\frac{ab(c+a-b)(b+c-a)}{4(a+b+c)^2} \\
&=\frac{abr^2}{(a+b+c)(a+b-c)} \\
&=\frac{abr^2}{(a+b)^2-(a^2+b^2-2ab\cos C)} \\
&=\frac{r^2}{2+2\cos C},
\end{align*}
而 $r$, $C$ 是定的，所以 $MJ\cdot MK$ 为定值，这就表明 $M$ 在一条双曲线上（可看成斜坐标系上的反比例函数）。

对于旁切圆的情形大概也差不多，暂时懒得写。