等边双曲线上四点的Ceva三角形的外接圆过其中心

hbghlyj

等边双曲线xy=1上任意四点\(P_i\)(i=1,2,3,4).\(P_1P_4\)与\(P_2P_3\)相交于点\(D_1\)，类似地定义\(D_2,D_3\).求证:\(D_1,D_2,D_3,D_4\)与坐标原点四点共圆
(单墫提供，2019.11.28)
类似于:外接圆一条直径的等角共轭像的中心在其上一点的塞瓦圆上

kuing

想起了这帖 kuing.cjhb.site/forum.php?mod=redirect&go … d=4449&pid=20222（不一定有关联）

力工

添一个上来。ABCD的Poncelet Point是O，等角共轭

kuing

回复 1# hbghlyj

用行列式倒不是难算。PS、没有 `D_4`。



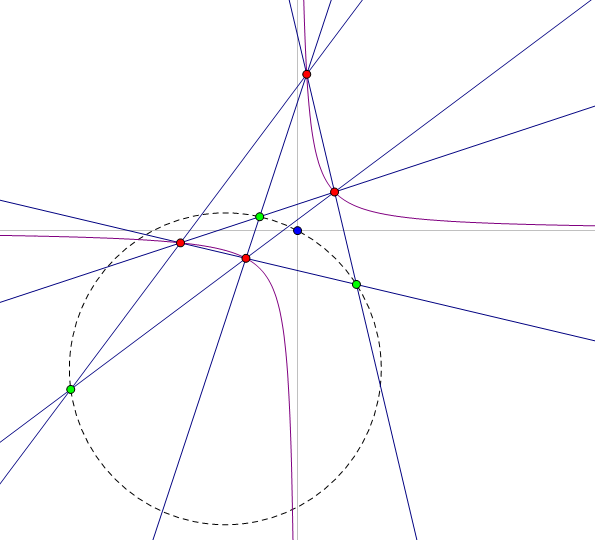
设 `P_1(a,a^{-1})`, `P_2(b,b^{-1})`, `P_3(c,c^{-1})`, `P_4(d,d^{-1})`，不难算出 `P_1P_2` 与 `P_3P_4` 的交点坐标为
\[\left( -abcd\frac{a^{-1}+b^{-1}-c^{-1}-d^{-1}}{ab-cd},\frac{a+b-c-d}{ab-cd} \right),\]
另外两个交点同理，为方便书写，记
\begin{align*}
m_1&=a^{-1}+b^{-1}-c^{-1}-d^{-1},&n_1&=a+b-c-d,\\
m_2&=a^{-1}+c^{-1}-b^{-1}-d^{-1},&n_2&=a+c-b-d,\\
m_3&=a^{-1}+d^{-1}-b^{-1}-c^{-1},&n_3&=a+d-b-c,
\end{align*}
即三个交点坐标为
\[\left( -abcd\frac{m_1}{ab-cd},\frac{n_1}{ab-cd} \right),\left( -abcd\frac{m_2}{ac-bd},\frac{n_2}{ac-bd} \right),\left( -abcd\frac{m_3}{ad-bc},\frac{n_3}{ad-bc} \right),\]
那么要证这三点及原点四点共圆，等价于证
\[
\begin{vmatrix}
-abcd\dfrac{m_1}{ab-cd} & \dfrac{n_1}{ab-cd} & \left( -abcd\dfrac{m_1}{ab-cd} \right)^2+\left( \dfrac{n_1}{ab-cd} \right)^2 \\
-abcd\dfrac{m_2}{ac-bd} & \dfrac{n_2}{ac-bd} & \left( -abcd\dfrac{m_2}{ac-bd} \right)^2+\left( \dfrac{n_2}{ac-bd} \right)^2 \\
-abcd\dfrac{m_3}{ad-bc} & \dfrac{n_3}{ad-bc} & \left( -abcd\dfrac{m_3}{ad-bc} \right)^2+\left( \dfrac{n_3}{ad-bc} \right)^2 \\
\end{vmatrix}=0,
\]
即证
\[
\begin{vmatrix}
m_1(ab-cd) & n_1(ab-cd) & (abcd)^2m_1^2+n_1^2 \\
m_2(ac-bd) & n_2(ac-bd) & (abcd)^2m_2^2+n_2^2 \\
m_3(ad-bc) & n_3(ad-bc) & (abcd)^2m_3^2+n_3^2 \\
\end{vmatrix}=0,
\]
注意到
\begin{align*}
m_1(ab-cd)-m_3(ad-bc)&=-(a-c)(b-d)(a^{-1}+b^{-1}+c^{-1}+d^{-1}),\\
n_1(ab-cd)-n_3(ad-bc)&=(a-c)(b-d)(a+b+c+d),\\
(abcd)^2m_1^2+n_1^2-\bigl( (abcd)^2m_3^2+n_3^2 \bigr)&=4(a-c)(b-d)(abcd+1),
\end{align*}
所以，上述行列式的第一行减第三行之后，可提出 `(a-c)(b-d)`，等价于证
\[
\begin{vmatrix}
-(a^{-1}+b^{-1}+c^{-1}+d^{-1}) & a+b+c+d & 4(abcd+1) \\
m_2(ac-bd) & n_2(ac-bd) & (abcd)^2m_2^2+n_2^2 \\
m_3(ad-bc) & n_3(ad-bc) & (abcd)^2m_3^2+n_3^2 \\
\end{vmatrix}=0,
\]
同理，第二行减第三行也将得出相同的结果，即减完后前两行相同，故行列式为零，得证。