双曲线的离心率

敬畏数学

双曲线$ \dfrac{x^2}{a^2}- \dfrac{y^2}{b^2}=1(a>0,b>0)$的左右焦点分别为$ F_{1}(-c,0)， F_{2}(c,0) $,直线$ x=m $交双曲线于$ A，B $两点，且$ AF_{2}⊥BF_{1} $,$ AF_{2}$交y轴于点$ M（0，-3b） $,则双曲线的离心率______。

kuing

Bao力计算吧……

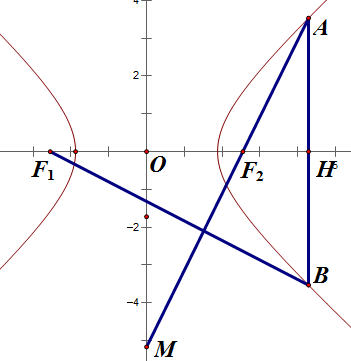
如图，设 `A(m,n)`，由相似，有
\[\frac{OM}{OF_2}=\frac{HA}{HF_2}=\frac{HF_1}{HB},\]即
\[\frac{3b}c=\frac n{m-c}=\frac{m+c}n,\]解得
\[m=\frac{c(9b^2+c^2)}{9b^2-c^2}, \, n=\frac{6bc^2}{9b^2-c^2},\]将其代入双曲线方程中，再代 `c=ea`, `b^2=(e^2-1)a^2` 进行化简，最终恰好能分解出
\[(5e^2-9)(20e^4-20e^2+9)=0,\]故 `e=3/\sqrt5`。

PS、“恰好能分解”言下之意是我试过将 `-3b` 改为一般的系数发现分解不了。

敬畏数学

回复 2# kuing
计算超级复杂。谢谢。