一个求角度题，30-20-10-20

abababa

已知$P$在$\triangle ABC$内，$\angle PBA=30^\circ,\angle PBC=20^\circ,\angle PCB=10^\circ,\angle PCA=20^\circ$，求$\angle PAB$。

在版主书里的求角度大帖里查了，人教论坛的看不到图，不知道有没有这个。这个简单的几何解法应该怎么解？

乌贼

这类题我一般是画出来的，虚线为等边三角形

abababa

回复 2# 乌贼

能发一下具体的作图顺序吗？我的作法是：作$\angle PBD=10^\circ$交$CP$于$D$，再作点$D$关于$BC,AC$的对称点$E,F$。

之后能求出$\triangle DBE$是正三角形，$\angle FEC$是正三角形，但怎么证明点$P$在$EF$上，点$A$在$FB$上？

zhcosin

目测似乎有$AP \perp BC$，先来证明这点吧，只要证明$A$和$P$在$BC$边上的投影重合就可以了。

注意到点$A$和点$P$都是由线段$BC$在两个端点处各自张成一个角度而相交得到的，于是考虑一个相关问题，如果在固定长度的线段$BC$的两个端点向同侧各自张成一个角度(B处的角记为$\alpha$，$C$处的角记为$\beta$)作两条射线相交于点$T$，来确定$T$在$BC$边上的位置。

由正弦定理就有
\[ \frac{TB}{\sin{\beta}} = \frac{BC}{\sin{(\alpha+\beta)}} \]
所以
\[ TB = \frac{\sin{\beta}}{\sin{(\alpha+\beta)}} BC \]
而它在$BC$边上的投影记为$T'$，则
\[ T'B=TB\cos{\alpha} = \frac{\sin{\beta}\cos{\alpha}}{\sin{(\alpha+\beta)}} BC = \frac{1}{1+\frac{\tan{\alpha}}{\tan{\beta}}} BC \]
于是为了证明$AP \perp BC$，只要证明分别确定点$A$和点$P$的两组$\frac{\tan{\alpha}}{\tan{\beta}}$相等就可以了，也就是证明恒等式
\[ \frac{\tan{20^{\circ}}}{\tan{10^{\circ}}} = \frac{\tan{50^{\circ}}}{\tan{30^{\circ}}} \]
证明应该是可以的，我还没搞出来。
证明之后就可以得到答案40度.

zhcosin

还有一个思路就是用角元形式的塞瓦定理可得
\[ \frac{\sin{\theta}}{\sin{(100^{\circ}-\theta)}}
\cdot \frac{\sin{20^{\circ}}}{\sin{30^{\circ}}}
\cdot \frac{\sin{20^{\circ}}}{\sin{0^{\circ}}} = 1\]
先证明$\theta=40^{\circ}$是这三角方程的解，再证明是唯一解。

kuing

回复 5# zhcosin

三角法多数人都会，楼主肯定也会，楼主是要纯几何解法……

乌贼

回复 3# abababa
先作等腰$\triangle BPE$，再延长至$D$则$\triangle BDE$为等边三角形，就没问题了

乌贼

写完，作等腰$ \triangle BPE $，再延长$ CP $至$ D $使$ BE=PE=ED $，则$ \triangle BDE $为等边三角形，再延长$ BA,EP $交于点$ F $有\[ \triangle FBE\cong \triangle CDE \riff \]$\triangle CEF $为等边三角形，故\[ \triangle CFA\cong \triangle CDE\riff AF=BE=EP \]
变为经典老题……

abababa

回复 8# 乌贼

仍然看不懂，作等腰$\triangle BPE$时，是作底角为$50^\circ$吗？之后怎么证明$\triangle BDE$是正三角形？能不能详细写一下啊，我没证出来

乌贼

回复 9# abababa
底角为$50\du$，$\triangle EPD$为顶角为$20\du$的等腰三角形，$\triangle BED$为顶角为$60\du$的等腰三角形即正三角形

isee

已知$P$在$\triangle ABC$内，$\angle PBA=30^\circ,\angle PBC=20^\circ,\angle PCB=10^\circ,\angle PCA= ...
abababa 发表于 2017-6-7 10:34

像是与链接forum.php?mod=viewthread&tid=2500中的4楼类似的——我没细想——只是像。
乌贼——特别是——他的辅助线。

abababa

回复 10# 乌贼


$\triangle EPD$是等腰三角形，是通过作图得出的，但顶角是$20^\circ$是怎么证明的？或者证明一个底角是$70^\circ$，这是怎么证明的？我都没证出来。

乌贼

回复 12# abababa
不会吧，$ \angle DPC= \angle BPE+\angle DPB=\angle BPE+\angle PBC+\angle PCB=50\du+20\du+10\du=80\du\riff \angle DEP=180\du-2\angle DPE=20\du$

abababa

回复 13# 乌贼

原来如此，辅助线太多了，总把等边三角形看成已知条件，结果推回来又发现是要证的。

abababa

回复 6# kuing

嗯，5楼的角元塞瓦定理方法还是以前在人教论坛学来的。

abababa

回复 11# isee

后来变成顶角是20度时就感觉出来和那帖相似了，一开始按主楼的图，我是做点$P$关于$AB$的对称点，但是没得出什么结果。

isee

回复 1# abababa


    想了想，我变来变去，实质是回到了这个最基础的出发点

题目：AB=AC, 角A=20度，AD=BC，求证角BDC=30度。

证明(by longnetpro)
以AC为边朝右作等边三角形ACE，易证ADE全等于ABC，于是AE=DE=EC，角ADE=80度，角AED=20度，角AEC=60度，所以角DEC=40度，角DEC=70度，角BDC=180度-80度-70度=30度。

当然，此题的证明方法很多，且都不算容易。

另外，值得注意的是，逆命题亦是成立的，即题目：AB=AC, 角A=20度，角BDC=30度，求证AD=BC。

而楼主的题，从某种方向来说，其实就是这个逆题而已。

结合主楼，给此逆命题一种并不算简单的证明——






要点：
1.三角形BCH是顶角为20度的等腰三角形。
2.等边三角形CDD'.
3.由角D'DC=2角D'PC，知点D为三角形D'PC的外心。
从而图中六条标记线段相等。


在此图上，回到原题




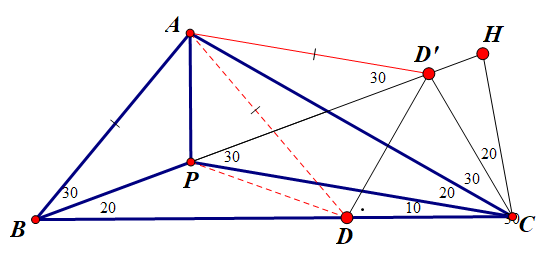
注意AC是线段DD'的中垂线，于是，AD=AD'.
再注意（用顶点B处的30度角……）ABCD'四点共圆，于是AB=AD'.

这样就得到了三角形ABP全等于三角形ADP，证毕。

abababa

回复 17# isee

看起来顶角是$20^\circ$的那个是最常见的情况。如果都是整数度，肯定是有限种情况，不知道是不是都有简单的平几证明，而且发现没有奇数度的情况，不知道是不是奇数度有什么特别。