抛物线切点弦相关问题

lemondian

这个问题用解析法解决不难，请问能不能用平几的方法解答？

kuing

非常简单，我们先看下面这个图：

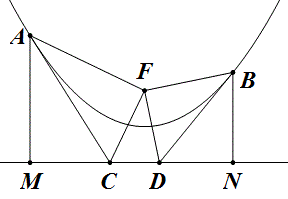
设两切线与准线交于 `C`, `D`，过 `A`, `B` 作准线的垂线，
则由光学性质及抛物线定义可得 `\triangle AFC\cong\triangle AMC`, `\triangle BFD\cong\triangle BND`，从而 `FA\perp FC`, `FB\perp FD`。
那么，当 `A`, `F`, `B` 三点共线时，必然有 `FC`, `FD` 重合，即 `C`, `D` 重合成 `E`，从而 `EF\perp AB`。
而且，我们还得到结论：`E` 在准线上；`EA\perp EB`。

lemondian

回复 2# kuing

感谢，感谢！