椭圆的切点弦的一个命题

lemondian

如图，点$P$为椭圆外的一点，过点$P$作椭圆的两条切线，切点分别为$T_1,T_2$，$O$为原点，则$OP$平分$T_1T_2$($即Q$是$T_1T_2$的中点)。

这个可以用切点弦方程联立直线OP硬算可证明。
请问：（1）有没有其它证法（特别是平几证法）？
（2）若不是一个标准型的椭圆，则点$P$与椭圆中心$O$的连线是否平分切点弦$T_1T_2$？若是，如何证明呢？

kuing

拉伸为椭圆显然成立啊

lemondian

回复 2# kuing
不用伸缩变换如何证明呢？

kuing

有了。借用《撸题集》P.519 的图：

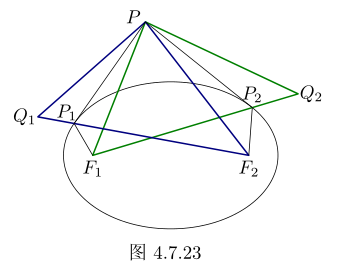
如上图，延长 `F_2P_1` 至 `Q_1` 使 `P_1F_1=P_1Q_1`，延长 `F_1P_2` 至 `Q_2` 使 `P_2F_2=P_2Q_2`，
由光学性质可得 `\triangle PQ_1F_2\cong\triangle PF_1Q_2`。
然后如下图：

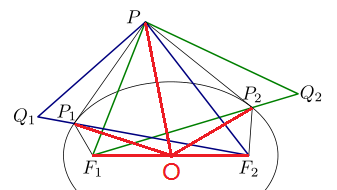
要证 `PO` 平分 `P_1P_2`，即证 `\S{POP_1}=\S{POP_2}`，由 `O` 是 `F_1F_2` 中点得
\[\S{POP_1}=\frac12(\S{PF_1P_1}+\S{PF_2P_1})=\frac12(\S{PQ_1P_1}+\S{PF_2P_1})=\frac12\S{PQ_1F_2},\]同理
\[\S{POP_2}=\frac12\S{PQ_2F_1},\]所以 `\S{POP_1}=\S{POP_2}`，即得证。

kuing

双曲线同理可证。

切点异支时：

\[\S{PP_1O}=\frac12(\S{PP_1F_2}-\S{PP_1F_1})=\frac12(\S{PP_1F_2}-\S{PP_1Q_1})=\frac12\S{PQ_1F_2},\]同理
\[\S{PP_2O}=\frac12\S{PQ_2F_1},\]所以 `\S{PP_1O}=\S{PP_2O}`，即 `PO` 平分 `P_1P_2`。

切点同支时也一样：

lemondian

回复 4# kuing

这个地方没看懂呢

kuing

回复 6# lemondian

…………

M 为 AB 中点，A、B 在 CD 同侧，则 `\S{MCD}=\frac12(\S{ACD}+\S{BCD})`。
这显不显然？

lemondian

回复 7# kuing
三个三角形的高恰为梯形中位线的关系？