Last edited by 2021-5-31 16:49抛物线$y^2$=2px(p>0)上不同的三点A,B,C处的切线两两相交于$P_1,P_2,P_3$,
设抛物线的焦点为F,则$ FA \cdot FB\cdot FC=F P_{1}\cdot F P_{2} \cdot F P_{3}. $
求一个几何证明
只需证如下结论:过P作抛物线的两条切线,切点为A,B,求证FP²=FA⋅FB.
Last edited by hbghlyj 2021-5-31 23:19
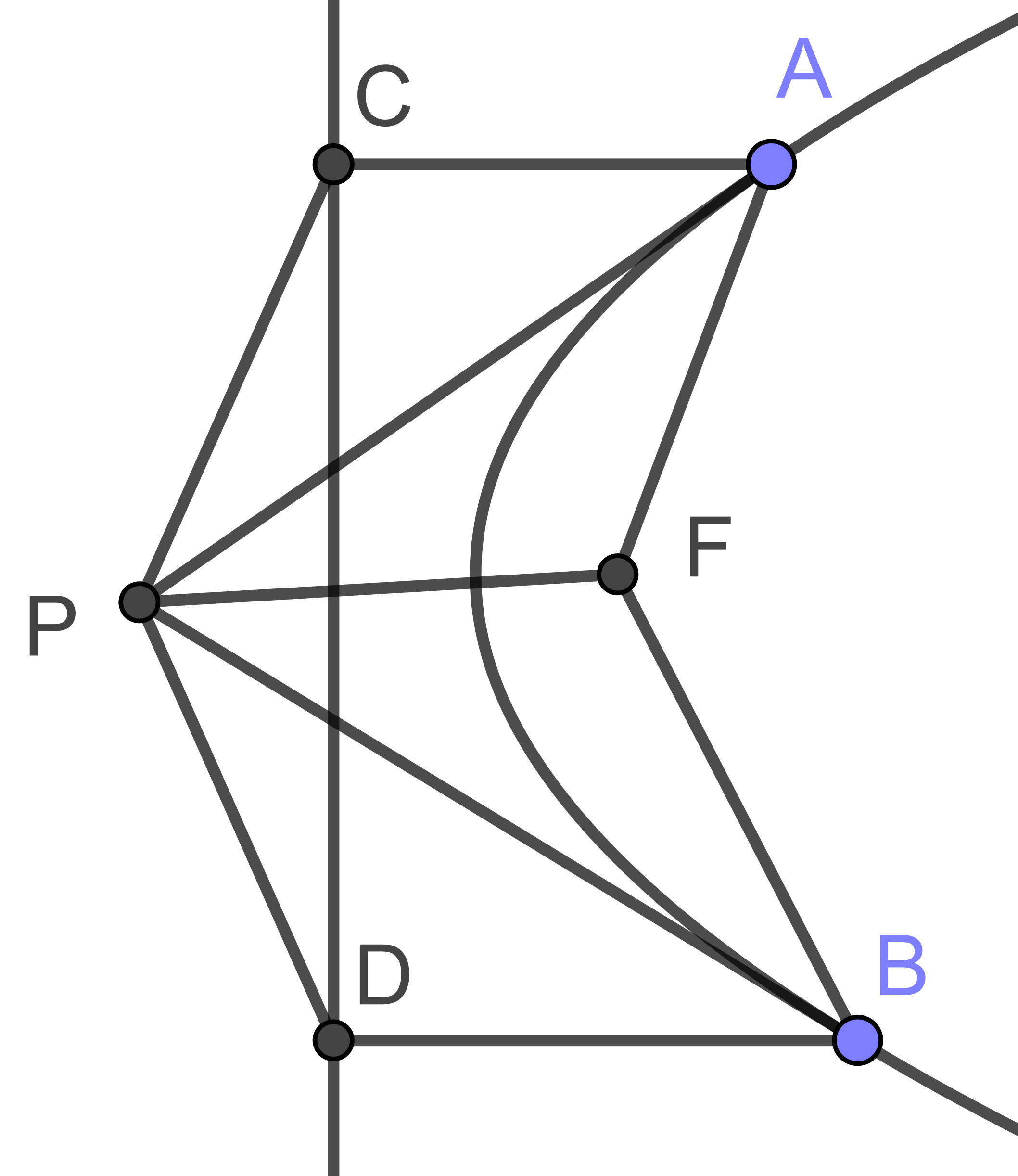
设A,B在准线上的投影为C,D,则AC=AF,BD=BF.由光学性质有AP平分∠CAF,所以AP垂直平分CF,CP=FP,同理DP=FP,所以CP=DP,∠CDP=∠DCP,故∠PFA=∠PCA=∠PDB=∠PFB,又2∠AFP+2∠APF+2∠BPF=∠ACP+∠PDB+∠CPD=360°,有∠AFP+∠APF+∠BPF=180°,即∠BPF=∠PAF,所以△AFP~△PFB,FP²=FA⋅FB.
kuing
posted 2021-5-31 23:52
