一道平几角度计算

wzyl1860

如图，$\triangle A B C$ 中，$\angle A C B=26^\circ$, $\angle A B C=51^{\circ}$, $C D$ 平分 $\angle A C B$, $\angle B A D=73^{\circ}$，连 $B D$，则 $\angle B D C=$

huing

证明一（同一法）。
我们通过以下作图重构四点形$ABCD$：
1、在BC边上作$\triangle{BCD'}$, 其内角$\angle B=17\du ,\angle C=13\du，\angle D'=150\du  $。$D'$与$D$在BC同侧。
2、作$\triangle{BCD'}$的BC边上的高$D'E$，将$\triangle{BCD'}$划成两个直角三角形。
3、将所得两直角三角形沿其斜边镜像过去。
4、再将所得两镜像三角形沿其较长直角边镜像到新的一侧。
得图如下

同一法作图

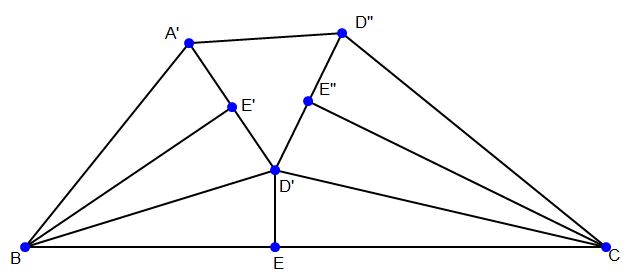
简单地计算角度，由作图法可知：
1、$\triangle{A'D'D''}$是一个正三角形，故$A',E'',C$三点共线。
2、$\angle A'BC=51\du ,\angle A'CB=26\du，\angle BA'D'=73\du  $
于是所得四点形$A'BCD'$与四点形$ABCD$重合，故$\angle BDC=150\du  $。

huing

证明二（直接法）
1、将$\triangle ACD$沿其最长边AC镜像出去，可得正三角形$\triangle ADD'$.
2、取$AD$的中点$E$，$AC$与$DD'$的交点$G$，得1/4正三角形$\triangle DEG$.
3、延长$CD'$和$BA$，取交点$F$, 计算角度可知$\angle F=90\du $

直接法

4、连接$FE，FG$，它们显然是$\angle F=90\du $的三等分线。
又由作图法知$CD$，$CG$是$\angle BCF$的三等分线。
故$\triangle DEG$是Rt$\triangle BCF$的莫莱三角形。
所以$BD$，$BE$也是$\angle B=51\du$的三等分线，$\angle CBD=17\du$.
于是最后得$\angle BDC=150\du$.

huing

本题以直角三角形的莫莱三角形为背景。

直角三角形的莫莱三角形的一条性质：两锐角近直角边的三等分线与莫莱三角形的对应边垂直。
即上楼的$BE\perp DE$，$CG\perp DG$。

hbghlyj

楼上的性质的证明