初中几何一题，求角

hbghlyj

P为△ABC内一点,∠ABC=60°,AP⊥PC,BP=PC,AP=BC,求证∠CBP=6°

三角法
证逆命题：P为△ABC内一点,∠ABC=60°,AP⊥PC,BP=PC,∠CBP=6°,则AP=BC
设$\frac{AP}{CP}=\frac{AP}{BP}=\frac{\sin 54°}{\sin24°}$,$\frac{BC}{CP}=2\cos6°$,只需证$\sin 54°=2\cos6°\sin24°$,由三倍角公式$\cos18° =4\cos 6°\cos54°\cos 66°$,$2\sin36°\cos36°=\sin72°=4\cos 6°\cos54°\sin 24°,\cos36°=2\cos 6°\sin 24°,\sin54°=2\cos 6°\sin 24°$
几何法(by 明天)
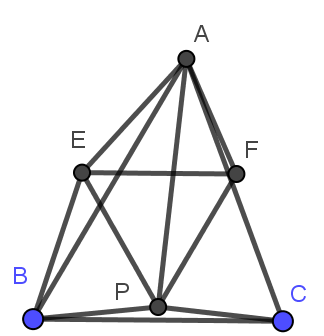
作等腰梯形ABPF并取其外接圆圆心E,设∠CBP=∠BCP=x,则∠ABP=60°-x,∠BAP=30°-x,∠EAB=∠EBA=2x,∠PEF=2∠PBF=2(∠PBA-∠ABF)=2(60°-x-30°+x)=60°$\Rightarrow$△EPF为正三角形$\Rightarrow$∠BEF+∠EBC=∠BEP+∠PEF+∠EBA+∠ABC=2∠BAP+∠PEF+∠EBA+∠ABC=2(30°-x)+60°+2x+60°=180°$\Rightarrow$EF$\parallel$BC，又PB=PC，∆PEF为正三角形$\Rightarrow$EFCB为等腰梯形$\Rightarrow$∠BCF=∠CBE=∠CBF+∠FBE=∠CBF+∠EFB=2∠CBF
又BC=AP=BF$\Rightarrow$∠BFC=∠BCF=2∠CBF，又∠BFC+∠BCF+∠CBF=180°$\Rightarrow$5∠CBF=180°$\Rightarrow$∠CBF=36°$\Rightarrow$x=∠CBP=∠CBF-∠PBF=36°-30°=6°

kuing

P为△ABC内一点,∠ABC=60°,AP=BC,AP⊥PB,求证：∠CAP=6°
hbghlyj 发表于 2020-1-30 18:02

缺条件吧？以目前的条件看这三角形都不能固定

hbghlyj

回复 2# kuing
不好意思。。这是考试后回忆题。。竟然搞错了。。考后失忆

hbghlyj

回复 2# kuing
好了。纯几何解法也有了。

乌贼

如图：分别作正$ \triangle BCD、\triangle APE $，$ PM、EN $分别为$ AE、AP $的垂直平分线，$ Q、F $为线段$ PM $上的两点且$ PF=PN、PQ=PA $有
   
   $ \triangle CPF $为正三角形，\[ CF=CP\riff \angle FDC=\angle PCB \]\[ AQ=EQ=AN=PN=CP=BP \]又\[ \angle QAN=60\du \riff QN=QE=QA\]即$ Q $为$ \triangle AEN $ 的外接圆圆心。因$ \angle PDB=\angle AEN=30\du  $，所以$ AEND $四点共圆，得\[ \angle EDN=\angle EAN\riff \angle EDF=30\du  \]及\[ \angle DQN=2\angle NAD=60\du -4\angle PCB \]又$ FNDQ $为等腰梯形，所以\[ \angle DQN=\angle FDQ\riff 60\du -4\angle PCB=30\du +\angle PCB\riff \angle PCB=6\du  \]

hbghlyj

回复 5# 乌贼
感谢回复。似应为PQ=PD而不是PQ=PA。

乌贼

如图：
   
      作$ BC $的垂直平分线$ PD $交$ AB $于$ D $，$ QF $为$ AP $的垂直平分线，作正$ \triangle AFE $。因为\[ AE=EF\\ \angle AEF=2\angle FDB=60\du  \]所以$ E $为$ \triangle ADF $外接圆圆心，得\[ ED=EF\riff \angle EDF=\angle EFD=60\du +2\angle PCB \]又\[ \triangle DBP\cong \triangle PAE(DB=PA,\angle DBP=\angle PAE,AE=BP)\\\riff PD=PE,\angle APE=30\du  \]故在$ \triangle PED $中\[ \angle EPD+\angle PDE+\angle PED=\angle EPD+2\angle PDE=30\du +\angle APD+120\du +4\angle PCB=180\du \\\riff \angle PCB=6\du  \]

hbghlyj

感谢回复。这就更清楚了。如果把△DBP≅∠PAE改成△DBP≅△PAE就完美了。