初中几何一题，求角

hbghlyj

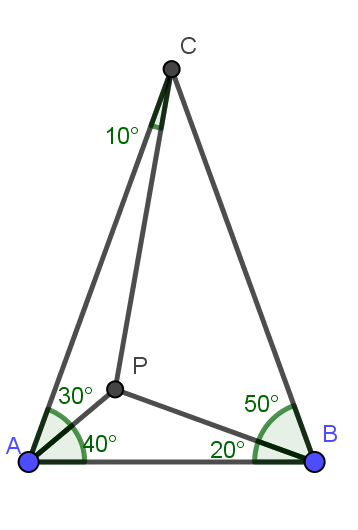
P是$\triangle ABC$内一点,$\angle BAP=40°,\angle CAP=30°,\angle ABP=20°,\angle CBP=50°,$求证：$\angle ACP=10°$



三角法
由角元塞瓦定理,$\sin^2 30°\sin20°=\sin 40°\sin50°\sin10°\Leftrightarrow \cos10°=2\sin40°\sin50°\Leftrightarrow \sin80°=2\sin40°\cos40°$
几何法
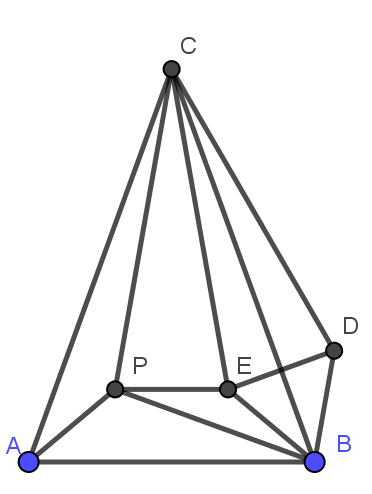
①作$\triangle BCD≌\triangle ACP≌\triangle BCE$,D,E分别在三角形外部和内部,$\because$BD=BE,∠DBE=60°,$\therefore \triangle BDE$是等边三角形,APEB是等腰梯形,$\angle PBE=\angle CBP-\angle CBE=20°=\angle ABP$,PE=AP=DE,CP=CD=CE,$\angle BCD=\frac12\angle DCE=\frac14\angle DCP=10°$
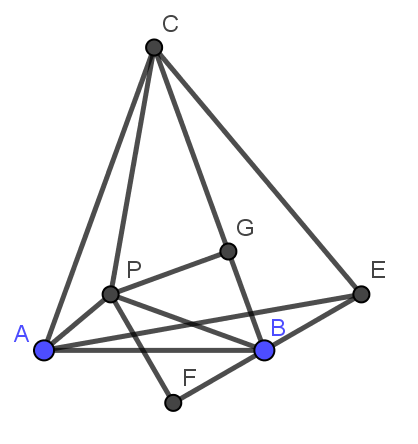
②作正$\triangle ACE$,B与E在AC同侧,$PF\bot BE$于F,$PG\bot BC$于G,AC=BC=EC,$\angle CBE=20°,\angle CBE=80°,\angle PBF=180°-80°-50°=50°=\angle PBG$,PF=PG,又AP平分$\angle CAE$,CP=EP,$\therefore\triangle CPG≌\triangle EPF,$BPCE共圆.$\angle PCB=\angle PCE-\angle BCE=\angle PBF-20°=30°,\angle ACP=40°-30°=10°$

isee

此题也是经典，对称的典范，今天也碰到了，在知乎提问.


题：等腰 $\triangle ABC$ 中 $AB=AC,$ 点 $P$ 为三角形内一点满足 $\angle ABP=30^\circ,\ $ $\angle PBC=40^\circ,\ $ $\angle BCP=20^\circ,$ 求 $\angle PAB.$





将 $\triangle ABP$ 沿 $AB$ 折叠得到 $\triangle AP_1B,$ 连接 $PP_1,$ 由 $\angle ABP=30^\circ$ 得正 $\triangle BPP_1.$ 注意到 $\angle BPC=120^\circ$ 与 $\angle P_1PB=60^\circ$ 互补，则 $P_1,\ P,\ C$ 三点是共线的.

另一方面将 $\triangle ABP$ 关于三角形 $ABC$ 的对称轴对称得到 $\triangle ACP_2,$ 连接 $PP_2,$ 则 $PP_2\parallel BC,$ 所以 $\angle P_2PC=\angle BCP=20^\circ=\angle P_2CP,$ 所以 $\bm {PP_2=CP_2}=PB=PP_1,$ 即点 $P$ 是 $\triangle BP_2P$ 的外心，则在等腰三角形 $P_1PP_2$ 中求得 $\color{blue}{\angle PP_2P_1=10^\circ}.$

又由对称可知 $AP_1=AP=AP_2$ 即点 $A$ 是 $\triangle P_1PP_2$ 的外心，于是 $\angle PAP_1=2\angle PP_2P_1=20^\circ,$ 从而 $\angle PAB=\frac 12\angle PAP_1=10^\circ,$ ( 则 $\angle PAC=30^\circ$).


这样就 OK 了.

事实上，$\angle P_2PC=\angle BCP=20^\circ $，再由即点 $A$ 是 $\triangle P_1PP_2$ 的外心，就可以得到结果了.





=================


其次，这个用赛瓦定理角元形式并不易（纯三角），记录一下吧.

记 $\angle BAP=x$ 则\[\frac {\sin 30^\circ}{\sin 40^\circ}\cdot \frac {\sin 20^\circ}{\sin 50^\circ}\cdot \frac {\sin (40^\circ-x)}{\sin x}=1,\]
\begin{align*}
\sin 20^\circ \sin (40^\circ-x)&=2\sin 40^\circ\cos 40^\circ\sin x\\
\sin 20^\circ \sin (40^\circ-x)&=\sin 80^\circ\sin x
\end{align*}
到这里之后，直接积化和差，没有出路.
另选两路，一是继续倍角公式
\begin{align*}
2\sin 10^\circ\cos 10^\circ \sin (40^\circ-x)&=\sin 10^\circ\sin x\\
\sin 10^\circ\sin (40^\circ-x)&=\sin 30^\circ\sin x
\end{align*}
再积化和差即解.


另一路是化为分式，合分比一下
\begin{align*}
\frac{\sin 20^\circ}{\sin 80^\circ} &=\frac {\sin x}{\sin (40^\circ-x)}\\[1em]
\frac{\sin 20^\circ+\sin 80^\circ}{\sin 20^\circ-\sin 80^\circ} &=\frac {\sin x+\sin (40^\circ-x)}{\sin x-\sin (40^\circ-x)}
\end{align*}
再分子分母四次和差化积，变成正切，再利用正切三倍角公式 $\tan 30^\circ =\tan 10^\circ\tan 50^\circ \tan 70^\circ,$ 见奇效，虽曲折点.

isee

P是$\triangle ABC$内一点,$\angle BAP=40°,\angle CAP=30°,\angle ABP=20°,\angle CBP=50°,$求证：$\a ...
hbghlyj 发表于 2020-1-31 10:39

②

实际上就是对称，导四点共圆，这个垂直太“初中”了