角 ACB=40 度，点 D 在 BC 边上满足角 DAC=60 度，若 BD=AC，求角 B

isee

源自知乎提问，（源链接）



题：点$D$为$\triangle ABC$上一点，满足$AC=BD$，若$\angle DAC=60^\circ$，$\angle ACB=40^\circ$，求角$\angle ABC$.












同一法，以 $AC$ 向下作正 $\triangle ACO$，如图所示 .


在 $BD$ 上取点 $B'$使 $OB'=OC(=AO=AC) $，即 $\angle DB'O=20^\circ $，由于$ \angle B'DO=80^\circ$ ，于是 $\angle B'OD=80^\circ=\angle BDO$ ，从而有 $B'D=(B'O=OC=AC=)BD$ ，即点 $B'$与点 $B$ 重合.
于是点 $O$ 是 $\triangle ABC$ 的外心，则 $\angle ABC=\frac 12\angle AOC=30^\circ$.

PS：构造正三角形等，在构造全等亦可，如在BD取点`E`使`\angle OED=80^\circ`证`\triangle OEC\cong \triangle ODB`.

isee

终于把这帖给找到了，我记得 Kuing 帮我把图擦干净的，否则不会坚持翻翻翻翻翻，哈哈



源自知乎提问，又解




题：如图 1 在三角形 ABC 中，角 ACB=40 度，点 D 在 BC 边上满足角 DAC=60 度，若 BD=AC，求角 B.

图 1



解：如图 1 所示作角 BCO=20 度交 AD 的延长线于点 O，则依题条件可知正三角形 AOC.

再以点 C 为圆心，以 CA 为半径作圆 C 交 BC 于点 E，则 EC=AC=BD.

连接 OE 则易知在圆 C 中角 EOA=角 ECA/2=20 度，又角 EDO=角 ADC=80 度，即有等腰三角形 OED 且顶角 EOD 为 20 度.

从而知 EO 为圆 CDO 的切线于是  这表明 DO 亦是圆 EBO 的切线，即角 CBO=角 DOE=20 度=角 BCO，从而 OB=OC=OA，即点 O 是三角形 ABC 的外心，所以角 B=角 AOC/2=30 度.

player1703

Mind Your Decisions 讲过mindyourdecisions.com/blog/2022/03/28/a-good- … es-triangle-problem/

等腰三角形$ABC$中$AB=AC$, $\angle A = 100\du$. 延长$AB$至$D$使得$AD=BC$. 求$\angle ADC$.
我的方法和Mind Your Decisions的思路很类似都是构造正三角形只是细节稍有不同:
以AD为边向上作正三角形$AED$, $\angle CAE = 100\du - 60\du = 40\du = \angle ACB$, $AE=AD=CB$, $AC=CA$, $\triangle CAE \cong \triangle ACB$, $CE=CA$, $ACED$是筝形 $CD$平分$\angle ADE$, $\angle ADC = 30\du$
然后这题和主楼的题有什么关系呢? 其实只要在$DB$上取点$E$使得$DE=DA$由于$\angle ADE = 100\du$ $\angle DEA = \angle DAE = 40\du = \angle C$, $AE = AC = BD$ 然后去掉右半边图形就和前面那题一样了


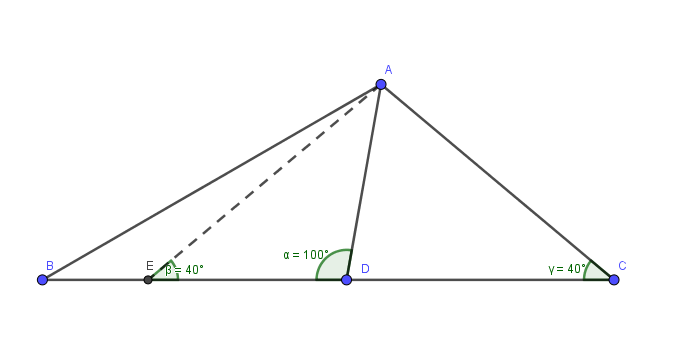
更新: kuing.cjhb.site/forum.php?mod=viewthread& … 2&extra=page%3D1
然后再补充一个三角解法:
类似链接里1楼解答可得:
\begin{equation*}
\cot B = \frac{1 + \sin40\du\cot80\du}{\sin40\du}
\end{equation*}
只要证:
\begin{align*}
1 + \sin40\du\cot80\du &= \sqrt3 \sin40\du \\
\iff \sin 80\du + \sin 40\du\cos 80\du &= \sqrt3 \sin 40\du\sin 80\du \\
\iff 2\sin 40\du\cos 40\du + \sin 40\du\cos 80\du &= \sqrt3 \sin 40\du\sin 80\du \\
\iff 2\cos 40\du + \cos 80\du &= \sqrt3 \sin 80\du \\
\iff \cos 40\du &= \frac{\sqrt3}{2} \sin 80\du - \frac{1}{2}\cos 80\du \\
\iff \cos 40\du &= \sin (80\du - 30\du)\\
\iff \cos 40\du &= \sin 50\du
\end{align*}
最后一行显然成立