来自人教群大前晚的一道绝对值题

kuing

辽爱好者-1bk3(2047******) 23:20:27

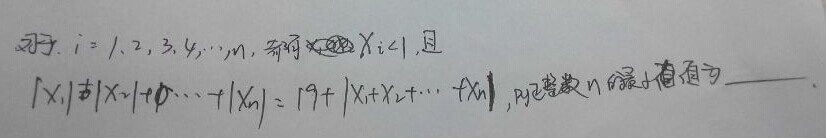
求教

话说这道题我做起来实在有点不安，不是因为题目难，而是因为题目是手抄的，并且两行字里居然就涂划了四个地方！可见其马虎程度……哎算了，既然闲着，还是玩玩吧……

题目：对于 $i=1$, $2$, \ldots, $n$，都有 $x_i<1$，且
\[\abs{x_1}+\abs{x_2}+\cdots+\abs{x_n}=19+\abs{x_1+x_2+\cdots+x_n},\]
则正整数 $n$ 的最小值为\tk 。

解：显然各 $x_i$ 不能全部同号，又易见当 $n$ 取最小值时，$x_i$ 中不会有 $0$，这是因为去掉为 $0$ 的项后已知等式左右两边的值不变，$n$ 就可以更小，故此，再由对称性，我们可以不妨设
\[1>x_1\geqslant x_2\geqslant \cdots \geqslant x_k>0>x_{k+1}\geqslant x_{k+2}\geqslant \cdots \geqslant x_n,\]
其中 $k\in\Bbb N^+$, $k<n$。

（1）若 $x_1+x_2+\cdots +x_n<0$，则已知等式化为
\[x_1+x_2+\cdots +x_k-x_{k+1}-x_{k+2}-\cdots -x_n=19-x_1-x_2-\cdots -x_n,\]
得到
\[\frac{19}2=x_1+x_2+\cdots +x_k<k\riff k\geqslant 10\riff n\geqslant 11;\]

（2）若 $x_1+x_2+\cdots +x_n\geqslant 0$，则有
\[-x_{k+1}-x_{k+2}-\cdots -x_n\leqslant x_1+x_2+\cdots +x_k<k,\]
已知等式化为
\[x_1+x_2+\cdots +x_k-x_{k+1}-x_{k+2}-\cdots -x_n=19+x_1+x_2+\cdots +x_n,\]
得到
\[\frac{19}2=-x_{k+1}-x_{k+2}-\cdots -x_n<k\riff k\geqslant 10\riff n\geqslant 11.\]

综合（1）（2）我们得到 $n\geqslant 11$，最后举一个 $n=11$ 的例子：$x_1=x_2=\cdots=x_{10}=0.95$, $x_{11}=-10$，它满足条件，所以 $n$ 的最小值就是 $11$。

chr93918

这就是数学思维

Tesla35

原题可能是下面图片所示，那人确实太马虎了
4．对于 $i=1,2, \cdots, n$ ，有 $\left|x_i\right|<1$ ，又假设
\[
\left|x_1\right|+\left|x_2\right|+\cdots+\left|x_n\right|=19+\left|x_1+x_2+\cdots+x_n\right|
\]
求整数 $n$ 的最小值．

4．因为
\[
\begin{aligned}
& \text { 因为 } \\
& 19=\left|x_1\right|+\left|x_2\right|+\cdots+\left|x_n\right|-\left|x_1+x_2+\cdots+x_n\right| \\
& \quad \leqslant\left|x_1\right|+\left|x_2\right|+\cdots+\left|x_n\right|<n
\end{aligned}
\]
所以，$n \geqslant 20$ ．
当 $n=20$ 时，取
\[
x_i=\left\{\begin{array}{l}
0.95, \quad \text { 当 } i \text { 为奇数时; } \\
-0.95, \text { 当 } i \text { 为偶数时. }
\end{array}\right.
\]
它们满足题设条件．故 $n$ 的最小值是 20 ．

爪机专用

回复 3# Tesla35

果然如此！
幸好少了绝对值也能做。
不过话说回来，有了那个绝对值变太简单了反而有点无趣，难道抄题的是改编？

乌贼

流行改编

kuing

因抄错题而无意中创造出的改编题而且比原题更有意思，这种事也见过不少次……

kuing

粤B爱好者T35(3705*****)  17:36:44
@粤A爱好者kuing✈
找到了题目来源

对于 $i=1,2, \cdots, n$ ，有 $\left|x_i\right|<1$ ，又设 $\left|x_1\right|+\left|x_2\right|+\cdots$ $+\left|x_n\right|=19+\left|x_1+\cdots+x_n\right|$ ．那么整数 $n$ 的最小值是多少？

【题说】第六届（1988 年）美国数学邀请赛题4．
【解】因 $\left|x_{i}\right|<1,\left|\sum_{i=1}^{n} x_{i}\right| \geqslant 0$ ，故
\[
19=\sum_{i=1}^{n}\left|x_{i}\right|-\left|\sum_{i=1}^{n} x_{i}\right| \leqslant \sum_{i=1}^{n}\left|x_{i}\right|<n
\]
另一方面，令 $x_1=x_2=\cdots=x_{10}=0.95, x_{11}=x_{12}=\cdots=x_{20}=-0.95$ ，则有
\[
\sum_{i=1}^{20}\left|x_{i}\right|=19,\left|\sum_{i=1}^{20} x_{i}\right|=0
\]
故 $n=20$ 即为所求最小值．

585果然不愧题库哥……