两个不会的解析几何，继续想~~双曲线等腰直角

realnumber

第七应该是三角形ABC,后面的记号是向量，估计是word没装mathtype.

realnumber

第7：设$\vv{AB}=\vv{b},\vv{AC}=\vv{c}$
$\abs{AO}=\abs{OC}=\abs{OB}$,即$\abs{\vv{AO}}=\abs{\vv{OA}+\vv{AC}}=\abs{\vv{OA}+\vv{AB}}$
两边平方得$0=2\vv{OA}·\vv{c}+\vv{c}^2=2\vv{OA}·\vv{b}+\vv{b}^2$.-----(1)
又$\vv{OG}·\vv{BC}=5$,即$(\vv{OA}+\frac{\vv{b}+\vv{c}}{3})·(\vv{c}-\vv{b})=5$----(2)
只需要把(1)代入(2).得到$\vv{b}^2-\vv{c}^2=30$.
然后是余弦定理，\[\cos{B}=\frac{c^2+a^2-b^2}{2ac}<0\]

同事王的做法：

kuing

7 see forum.php?mod=viewthread&tid=3411

realnumber

同事韩在BC上做投影,也可以方便解决

realnumber

回复 3# kuing


    恩,还有8,好难~~~

kuing

设左焦点 $F'$，连结 $F'A$, $F'B$，则 $F'AFB$ 显然为矩形，故 $AB=FF'=2c$，且 $FB-FA=F'A-FA=2a$。

设 $FA=x$, $FB=FC=y$，则有
\[\led
y-x&=2a,\\
x^2+y^2&=(2c)^2,
\endled\]
故
\[xy=\frac{x^2+y^2-(x-y)^2}2=2c^2-2a^2,\]
则
\[x+y=\sqrt{x^2+y^2+2xy}=2\sqrt{2c^2-a^2},\]
又由熟知结论有
\[\frac1x+\frac1y=\frac{2a}{b^2},\]
代入上面的结果即
\[\frac{\sqrt{2c^2-a^2}}{c^2-a^2}=\frac{2a}{c^2-a^2},\]
所以
\[2c^2-a^2=(2a)^2,\]
解得
\[e=\sqrt{\frac52}.\]

realnumber

上面有结论$\frac{1}{x}+\frac{1}{y}=\frac{2a}{b^2}$，用极坐标可以证明
$ρ=\frac{ep}{1-e\cos{\theta}},p=\frac{b^2}{c}$,不利用这个，怎么处理？
因为浙江教材删掉这个很久了.

其妙

8题：

kuing

上面有结论$\frac{1}{x}+\frac{1}{y}=\frac{2a}{b^2}$，用极坐标可以证明
$ρ=\frac{ep}{1-e\cos{\theta}},p=\frac{b^2}{c}$,不利用这个，怎么处理？
因为浙江教材删掉这个很久了.
realnumber 发表于 2015-4-20 23:29

极坐标表达式是用第二定义推的，所以用第二定义可以处理。

kuing

回复 8# 其妙

oh，这个更好，不用其他结论

PS、话说你也变成手稿党啦？

kuing

上面有结论$\frac{1}{x}+\frac{1}{y}=\frac{2a}{b^2}$，用极坐标可以证明
$ρ=\frac{ep}{1-e\cos{\theta}},p=\frac{b^2}{c}$,不利用这个，怎么处理？
因为浙江教材删掉这个很久了.
realnumber 发表于 2015-4-20 23:29

楼主的题既然可以像8#那样做，那么这个结论跟那个解法也应该有一定的相通性，于是由8#的辅助线，马上可以发现用余弦定理就能推出 $1/x+1/y=2a/b^2$ 这个结论，由
\begin{align*}
0&=\cos \angle AFF'+\cos (\pi -\angle AFF') \\
& =\frac{x^2+(2c)^2-(2a+x)^2}{4cx}+\frac{y^2+(2c)^2-(2a+y)^2}{4cy} \\
& =\frac{(c^2-a^2)(x+y)-2axy}{cxy},
\end{align*}
即得
\[\frac1x+\frac1y=\frac{x+y}{xy}=\frac{2a}{c^2-a^2}=\frac{2a}{b^2}.\]

realnumber

回复 9# kuing
第二定义一样从教材消失了.

realnumber

回复 8# 其妙
鼓掌~~~~

kuing

回复 12# realnumber

那就用11#的余弦定理好了

其妙

回复  其妙

oh，这个更好，不用其他结论

PS、话说你也变成手稿党啦？ ...
kuing 发表于 2015-4-21 00:59

那就来word版的：

kuing

回复 15# 其妙

嗯，这样清楚多了
要是有代码版就更好了

isee

回复 16# kuing
这代码根本不是问题，问题是其妙搞不定那图，纯tex下。

敬畏数学

回复 8# 其妙
这个做法就是了。

isee

源自知乎提问，经典题再现


题：点 $P$ 在双曲线右支上，过双曲线右焦点 $F$ 的直线 $PR$ 交双曲线另一点 $R$ ，点 $Q$ 与 $P$ 关于原点对称， 若$QF\perp PR$ 且 $QF=2FR,$ 求双曲线 $x^2/a^2-y^2/b^2=1$ 的离心率.





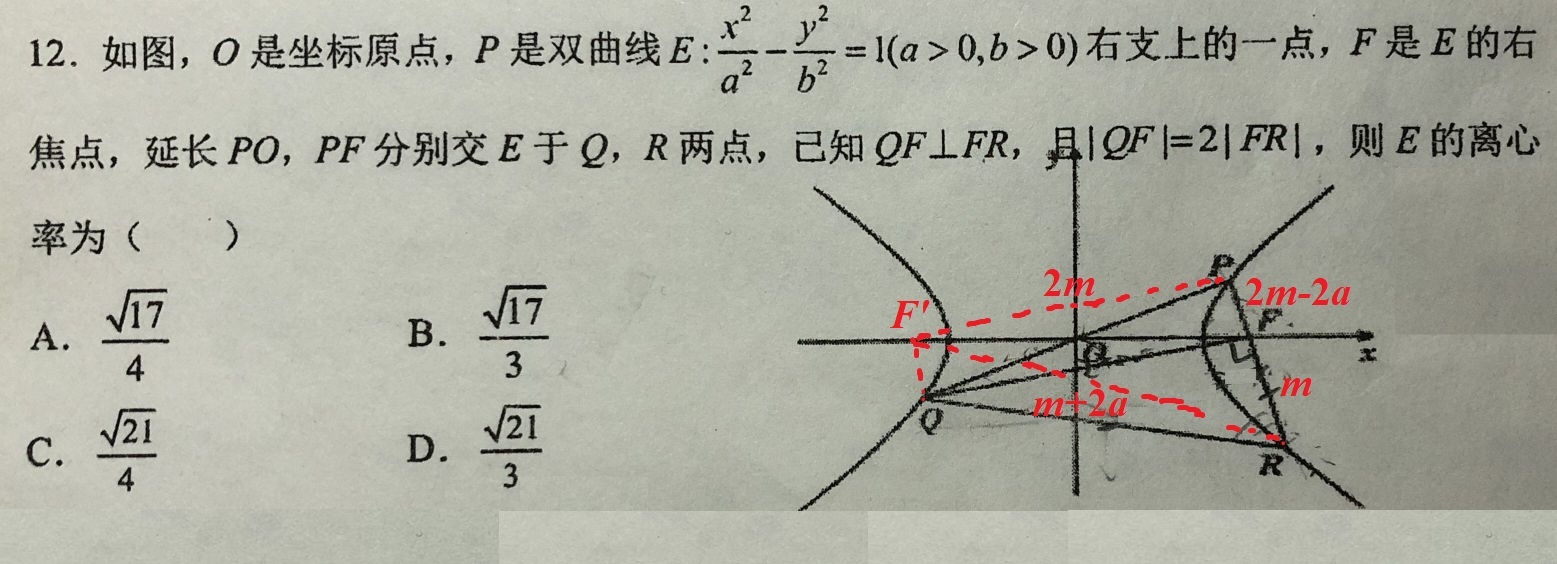
题中过右焦点 $F$ 才是此题的主要矛盾.

记 $F'$ 为双曲线的左焦点，依题条件则易知 $PFQF'$ 是矩形.

令 $QF=2FR=2m,$ 则 $PF'=2m,$ 再由双曲线第一定义有 $PF=2m-2a,$ $RF'=m+2a.$

于是在 $\mathrm {Rt}\triangle PF'R$ 中由勾股定理

$$4m^2+(3m-2a)^2=(m+2a)^2,$$ 化简即 $$2a=\frac {3m}2.$$

从而在 $\mathrm {Rt}\triangle PF'F$ 中 $$2c=F'F=\sqrt {4m^2+\left(2m-\frac {3m}2\right)^2}=\frac {\sqrt {17}m}2.$$

故 $$e=\frac ca=\frac {\sqrt {17}}3.$$

由此可以看到 $k_{PF}=-4,$ 但 $k_{QR}$ 的斜率并不易求得.

但可以求，考查直线 $PR,QR$ 的到角 $$2=\tan FRQ=\frac {k_{QR}-k_{PF}}{1+k_{QR}\cdot k_{PF}}=\frac {k_{QR}+4}{1-4k_{QR}},$$ 得 $$k_{QR}=-\frac 29.$$


PS：直线 $l_1,l_2$ 的斜率分别为 $k_1,k_2$ 则 $l_1$ 到 $l_2$ 的到角 $\alpha$ 满足： $$\tan\alpha =\frac{k_2-k_1}{1+k_1k_2}.$$

路在脚下

回复 19# isee


    学习了