最佳常数p使$x^2-x^3\geq y^4-y^3→\frac{x^p+y^p}2\leq1$

hbghlyj

求最小的正数p,使得对任何正数x,y满足$x^2-x^3\geq y^4-y^3$,都有$\frac{x^p+y^p}2\leq1$
我们已证明p=3时满足条件,而p=6时满足不了。。

kuing

用软件研究了下，应该是解不出精确解的，大概在 5.873 左右

hbghlyj

回复 2# kuing
取p=5用人工方法做做看？
对任意正数x,y满足$x^2+y^3\geq x^3+y^4$,求证$x^5+y^5\leq2$

kuing

回复 3# hbghlyj

考虑其逆否命题：任意正数 `x`, `y`，若 `x^5+y^5>2`，则 `x^2+y^3<x^3+y^4`。

而这只需证
\[\sqrt[5]{\frac{x^5+y^5}2}\cdot x^2+y^3\leqslant x^3+y^4\sqrt[5]{\frac2{x^5+y^5}},\]令 `x=ty`，则化为证明对任意正数 `t` 有
\[f(t)=t^3-1+\sqrt[5]{\frac2{t^5+1}}-\sqrt[5]{\frac{t^5+1}2}\cdot t^2\geqslant 0,\]这样就转化为一元函数问题，用软件画图看了下是成立的，但要人工证明看来还是有点困难，暂且休息一下。

回头看看 2# 的数值，如果是正确的话，那将上述函数的 5 改成 5.873 也是成立的，再用软件画图看是这样的：

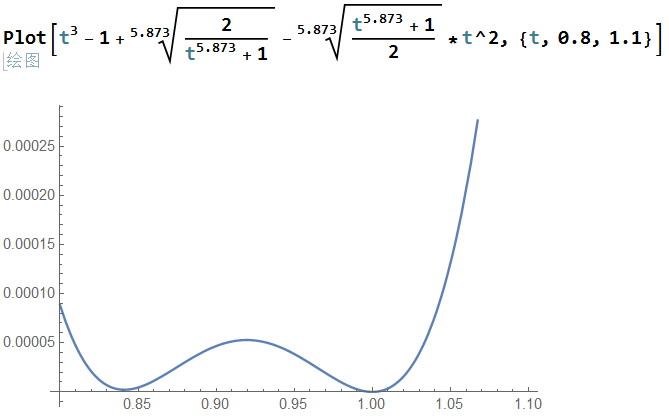
可以看到，除了 `t=1` 为零之外，在 0.85 附近也非常接近零，可见该最佳值估算应该是没问题的。

未完待续……