|
|
 kuing
kuing
posted 2021-5-25 23:54
相当于证明 `OH\cdot OG` 为定值,于是沿 `y` 轴方向将图形拉伸,使椭圆变为圆,并不改变结论。
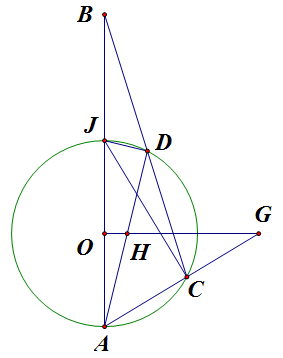
如上图,记圆半径为 `r`,则
\[\frac{OH\cdot OG}{r^2}=\tan\angle OAH\cdot\tan\angle OAG=\frac{DJ}{DA}\cdot\frac{CJ}{CA},\]注意 `\angle DJC=\angle DAC`,则有
\[\frac{DJ\cdot CJ}{DA\cdot CA}=\frac{\S{JCD}}{\S{ACD}}=\frac{BJ}{BA},\]从而
\[OH\cdot OG=r^2\cdot\frac{BJ}{BA},\]即为定值。
回到原题,椭圆是 `x^2/2+y^2=1`,`BJ/BA=1/3`,所以 `OH\cdot OG=2/3`,可知面积之积就是 `1/2`。 |
|