椭圆 求证轨迹为圆

hbghlyj

(1)点A与B分别是椭圆的右顶点与上顶点.
∠DOE=90°,AO是∠DOE的角平分线.
AB∥DE,DE交AO于C.
点C'在椭圆上,点D'在C'O上,AO是∠C'OE'的角平分线.
CO=C'O,DO=D'O,EO=E'O.
M是D'E'的中点.
求证:
M的轨迹是圆.

(2)点A与B分别是椭圆的右顶点与上顶点.
∠DOE=90°,AO是∠DOE的角平分线.
AB∥DE,DE交BO于C.
点C'在椭圆上,点D'在C'O上,AO是∠C'OE'的角平分线.
CO=C'O,DO=D'O,EO=E'O.
M是D'E'的中点.
求证:
M的轨迹是圆.

kuing

先看下图：

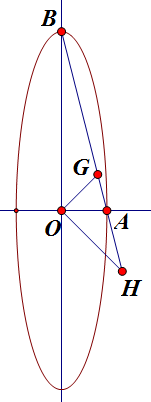
这里 `OG`, `OH` 均为平分线，由张角定理有
\[\led
\frac1a+\frac1b&=\frac{\sqrt2}{OG},\\
\frac1{OG}+\frac1{OH}&=\frac{\sqrt2}a
\endled\riff\led
OG&=\frac{\sqrt2ab}{a+b},\\
OH&=\frac{\sqrt2ab}{b-a},
\endled\]那么对于楼主第一个图的 `\triangle ODE` 及 `C`，由于和上图相似，于是有
\[OD:OE:OC=\frac{\sqrt2b}{a+b}:\frac{\sqrt2b}{b-a}:1,\]然后那个三角形就没用了，赶紧擦掉，剩下：

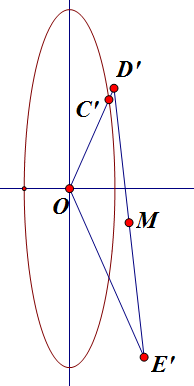
问题即为：`C'` 在椭圆上，`D'` 在直线 `OC'` 上，短轴平分 `\angle D'OE'`，且满足  `OD':OE':OC'=\frac{\sqrt2b}{a+b}:\frac{\sqrt2b}{b-a}:1`，求 `D'E'` 中点 `M` 的轨迹。

这样就是常规问题了，设 `C'(x,y)`，则
\[D'\left( \frac{\sqrt2b}{a+b}x,\frac{\sqrt2b}{a+b}y \right),\,E'\left( \frac{\sqrt2b}{b-a}x,-\frac{\sqrt2b}{b-a}y \right),\]那么
\begin{align*}
x_M&=\frac12\left( \frac{\sqrt2b}{a+b}+\frac{\sqrt2b}{b-a} \right)x=\frac{\sqrt2b^2}{b^2-a^2}x,\\
y_M&=\frac12\left( \frac{\sqrt2b}{a+b}-\frac{\sqrt2b}{b-a} \right)y=-\frac{\sqrt2ab}{b^2-a^2}y,
\end{align*}平方相加
\[x_M^2+y_M^2=\frac{2b^4}{(b^2-a^2)^2}x^2+\frac{2a^2b^2}{(b^2-a^2)^2}y^2=\frac{2a^2b^4}{(b^2-a^2)^2}\left( \frac{x^2}{a^2}+\frac{y^2}{b^2} \right)=\frac{2a^2b^4}{(b^2-a^2)^2}.\]

第二个估计也类似，就不再撸了