抽象函数的性质

lrh2006

（多选）已知f(x)为非常值函数，若对任意实数x,y均有$ f(x+y)=\frac{f(x)+f(y)}{1+f(x)\cdot f(y)} $，且当x>0时，f(x)>0，则下列说法正确的有（ ）
A.f(x)为奇函数  B.f(x)是$ (0，+\infty) $上的增函数  C.|f(x)|<1  D.f(x)是周期函数

kuing

假设存在 `x_0` 使得 `f(x_0)=1`，则令 `y=x_0` 得到 `f(x+x_0)=1` 对任意 `x` 恒成立，不符合“非常值”，所以这样的 `x_0` 不存在。同理可证不存在 `x_0` 使得 `f(x_0)=-1`。

令 `x=y=0` 得 `f(0)=\frac{2f(0)}{1+f(0)^2}` 解得 `f(0)=0` 或 `\pm1`，刚才已经证明了 `f(x)\ne\pm1`，所以只能 `f(0)=0`，然后令 `y=-x` 得 `f(x)+f(-x)=0`，所以是奇函数，A 正确。

对任意非零 `x`，由均值有
\[\abs{f(2x)}=\abs{f(x+x)}=\frac{2\abs{f(x)}}{1+f(x)^2}<\frac{2\abs{f(x)}}{2\sqrt{f(x)^2}}=1,\]
（均值不能取等同样是因为 `f(x)\ne\pm1`）所以 C 正确。

对任意正数 `x`, `y`，有
\[f(x+y)-f(x)=\frac{f(x)+f(y)}{1+f(x)f(y)}-f(x)=\frac{f(y)(1-f(x)^2)}{1+f(x)f(y)},\]
由 C 正确知上式为正，所以 `f(x+y)>f(x)`，因此 B 也正确。

由 B 正确知 D 错。

最后还需画蛇添足说明此题不是错题：不难验证 `f(x)=\tanh x=(e^x-e^{-x})/(e^x+e^{-x})` 满足条件，所以题目正确。

lrh2006

kuing 发表于 2023-2-4 17:16
假设存在 `x_0` 使得 `f(x_0)=1`，则令 `y=x_0` 得到 `f(x+x_0)=1` 对任意 `x` 恒成立，不符合“非常值”， ...

我起先不能排除$ f(0)\ne\pm1 $，所以写不下去了
kk竟然还能找到函数模型，好佩服

kuing

lrh2006 发表于 2023-2-4 21:25
我起先不能排除$ f(0)\ne\pm1 $，所以写不下去了
kk竟然还能找到函数模型，好佩服 ...

因为了解过双曲函数😉
它们和三角函数很像的，各种和差公式基本上就差个符号。

lrh2006

嗯嗯，已经科普了哈哈哈
这个函数模型也可以是$ f(x)=\frac{a^x-1}{a^x+1}(a>1) $
今天看到别人的讨论，觉得还是kk的解析写得最漂亮，一直都是最好的嘿嘿

kuing

lrh2006 发表于 2023-2-6 22:56
嗯嗯，已经科普了哈哈哈
这个函数模型也可以是$ f(x)=\frac{a^x-1}{a^x+1}(a>1) $
今天看到别人的讨论，觉 ...

`\tanh x` 也是这种形式的呀
\[\tanh x=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1}\]

hbghlyj

初中数学奥林匹克实用教程 第2册,叶军编著,长沙：湖南师范大学出版社 和第3讲的第22题比较像

22. 提示: $\sqrt{f(x)}=\frac{2^{x}-2^{-x}}{2^{x}+2^{-x}}$

hbghlyj

kuing 发表于 2023-2-6 16:00
`\tanh x` 也是这种形式的呀
\[\tanh x=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1}\] ...

$$f'(x)=\lim_{y\to0}\frac{f(x+y)-f(x)}y=\lim_{y\to0}\frac{f(y)[1-f(x)^2]}{y[1+f(x)\cdot f(y)]}$$
由2#证的$f(0)=0$知$\lim_{y\to0}[1+f(x)\cdot f(y)]=1$
$$f'(x)=\lim_{y\to0}\frac{f(y)[1-f(x)^2]}y=f'(0)[1-f(x)^2]$$
由WolframAlpha解得$$f(x)=\frac{e^{2 c x}-1}{e^{2 c x}+1}\qquad c=f'(0)$$

hbghlyj

由WolfreeAlpha得Step-by-step solution

Solve the separable equation ${\frac{\rmd f(x)}{\rmd x}\over-f(x)^2 + 1} = c$, such that $f(0) = 0$: Integrate both sides with respect to $x$: \[\int{{\rmd f(x)\over\rmd x}\over-f(x)^2 + 1}\rmd x = \int c\rmd x\] Evaluate the integrals: \[-\frac12\log(-f(x) + 1) + \frac12 \log(f(x) + 1) = c x + k_1\] Solve for $f(x)$: \[f(x) = {e^{2 (c x + k_1)} - 1\over e^{2 (c x + k_1)} + 1}\] Solve for $k_1$ using the initial conditions: Substitute $f(0) = 0$ into $f(x) = {e^{2 (c x + k_1)} - 1\over e^{2 (c x + k_1)} + 1}$: \[{e^{2 k_1} - 1\over e^{2 k_1} + 1} = 0\] Solve the equation: \[k_1 = 0\quad|\quad k_1 = i π\] Substitute $k_1 = 0$ into $f(x) = {e^{2 (c x + k_1)} - 1\over e^{2 (c x + k_1)} + 1}$: \[f(x) = \frac{e^{2 c x} - 1}{e^{2 c x} + 1}\] Substitute $k_1 = i π$ into $f(x) = {e^{2 (c x + k_1)} - 1\over e^{2 (c x + k_1)} + 1}$: \[f(x) = \frac{e^{2 c x} - 1}{e^{2 c x} + 1}\] Answer:\[ \bbox[5px,#e8faff,border:2px solid #add8e9]{f(x) = {e^{2 c x} - 1\over e^{2 c x} + 1}}\]

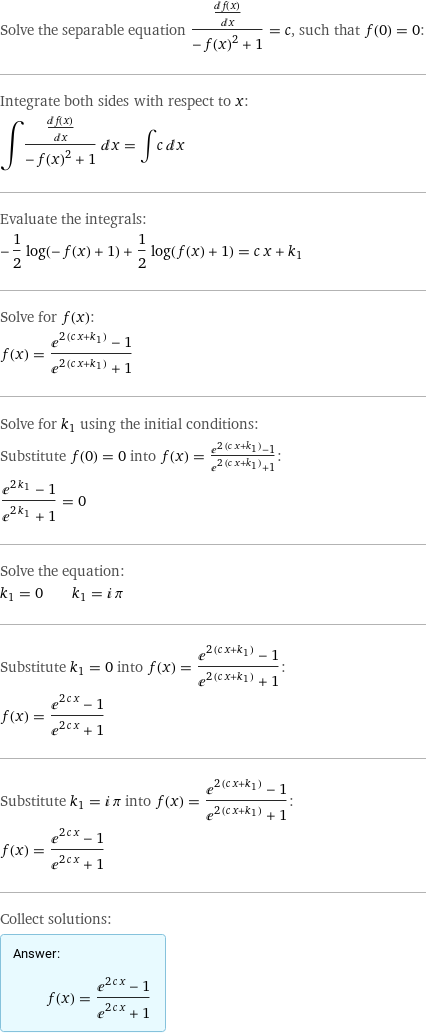
kuing

hbghlyj 发表于 2023-2-6 23:40
$$f'(x)=\lim_{y\to0}\frac{f(x+y)-f(x)}y=\lim_{y\to0}\frac{f(y)[1-f(x)^2]}{y[1+f(x)\cdot f(y)]}$$
...

那你还得先证明 `f'(0)` 存在

kuing

@hbghlyj
其实可以转化为柯西方程：
由于已经证明了 `\abs{f(x)}<1`，则存在 `g(x)` 使得
\[f(x)=\frac{e^{g(x)}-1}{e^{g(x)}+1},\]
代入条件等式中化简有
\[f(x+y)=\frac{f(x)+f(y)}{1+f(x)f(y)}\iff\frac{e^{g(x+y)}-1}{e^{g(x+y)}+1}=\frac{e^{g(x)}e^{g(y)}-1}{e^{g(x)}e^{g(y)}+1},\]
可见
\[g(x+y)=g(x)+g(y),\]
由已知条件，当 `x>0` 时 `f(x)>0`，即 `e^{g(x)}>1`，即 `g(x)>0`，这个条件是足够确定 `g(x)=g(1)x` 的，简略证明如下：
记 `g(1)=k`，易证对 `x\inQ` 有 `g(x)=kx`，当 `x>y` 时 `g(x)-g(y)=g(x-y)>0`，即 `g(x)` 单调增，对任意无理数 `\alpha`，设 `\an`, `\bn` 分别为单调增和单调减的无穷有理数列且都趋向 `\alpha`，则 `ka_n=g(a_n)<g(\alpha)<g(b_n)=kb_n`，令 `n\to\infty` 由夹逼定理即得 `g(\alpha)=k\alpha`，得证。

因此楼主这题其实是完全可以确定 `f(x)` 就只有 5# 的一种形式。

hbghlyj

• 若$f(x)$是一个解, 则$-f(x)$也是解.$$-{e^{2 c x} - 1\over e^{2 c x} + 1}={1-e^{2 c x} \over1+ e^{2 c x}}={e^{-2 c x} -1\over e^{-2 c x}+1}$$
• 当$c\to0$的极限$$f_0(x)=\begin{cases}1&x>0\\0&x=0\\-1&x<0\end{cases}$$是通分得的函数方程$f(x+y)[1+f(x)f(y)]=f(x)+f(y)$的解.
• 令$t(x)=\frac1{\sqrt p}\,f(x)$得函数方程$t(x+y)=\frac{t(x)+t(y)}{1+p\,t(x)t(y)}$的解$$t(x)=\frac1{\sqrt p}\cdot{e^{2 c x} - 1\over e^{2 c x} + 1}$$见此帖

lrh2006

kuing 发表于 2023-2-6 23:00
`\tanh x` 也是这种形式的呀
\[\tanh x=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1}\] ...

好吧，当我没说😛