|
|
 kuing
kuing
posted 2021-1-28 23:31
这题有可能是个非常坑爹的题,事关第二问可能根本和椭圆没有半毛钱关系,而第一问又是常识……
首先把椭圆和坐标系擦掉,简化为如下平几题:
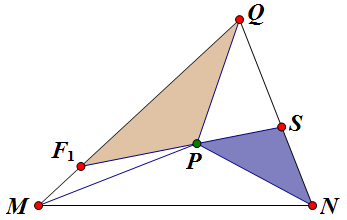
如图,线段 `F_1S` 两端在两边上且过重心 `P`,求那两块面积比的最小值。
设 `QM=mQF_1`, `QN=nQS`,则 `m`, `n>1` 且易证 `m+n=3`,因此
\begin{align*}
\frac{S_1}{S_2}&=\frac{S_1}{\S{QMP}}\cdot\frac{\S{QNP}}{S_2}\\
&=\frac{QF_1}{QM}\cdot\frac{QN}{SN}\\
&=\frac{QF_1}{QM}\cdot\frac{QN}{QN-QS}\\
&=\frac1m\cdot\frac n{n-1}\\
&=\frac{3-m}{m(2-m)}\\
&=\frac12\left( \frac3m+\frac1{2-m} \right),
\end{align*}由于 `1<m<2`,故由 CS 得
\[\frac{S_1}{S_2}\geqslant\frac{\bigl(\sqrt3+1\bigr)^2}4=1+\frac{\sqrt3}2,\]当且仅当 `m=3-\sqrt3` 时取等。
回到原题,如果能够找到使 `m=3-\sqrt3` 的点 `Q`,那么这个椭圆就是废的……
(所以我开头只是说“可能”,因为我还没去找这个点,说不定是不存在的,不过就算是这样,那至少问题也转化为求 `m` 的范围就好,不过我感觉存在的可能性应该大,时间关系晚点再试) |
|