椭圆压轴题

hao124

椭圆 $\Gamma: \frac{x^2}{4}+y^2=1, A\left(6, \frac{1}{6}\right)$ 为椭圆外一定点，点 $P$ 在椭圆上．过 $A$ 作直线 $l_1$ 交椭圆 $\Gamma$ 于 $B, C$ 两点，若存在过 $P$ 的定直线 $l_2$ 满足直线 $B P, C P$ 始终关于直线 $l_2$ 对称，则直线 $l_2$ 的斜率为 $\qquad$

isee

回复 1# hao124


    哇，拿GGB试了几个特殊值，搞不定~

kuing

取特殊情况猜一下 `P` 会在哪里。

过 `A` 作椭圆的两切线，切点分别为 `M`, `N`。

假设 `P` 在 `M` 处，则当 `l_1` 无限接近 `AN`，此时 `B`, `C` 趋向 `N`，那么 `l_2` 只能是 `MN` 或者垂直于 `MN` 于 `P`。
垂直于 `MN` 于 `P` 的那条线与椭圆有另一交点，现在，让 `l_1` 过该点，如下图，显然此时 `PB`, `PC` 并不关于 `MN` 对称，故此这种情况不满足题意。



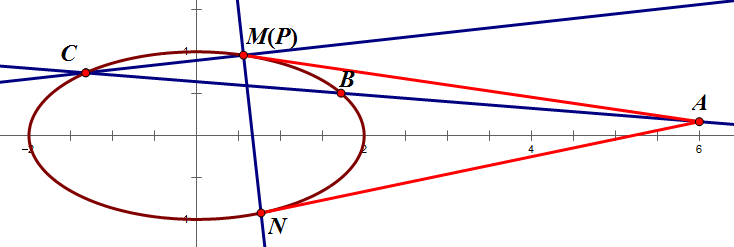
同理可证 `P` 在 `N` 处也不满足。

现在考虑 `P` 不在 `M` 或 `N` 处时。



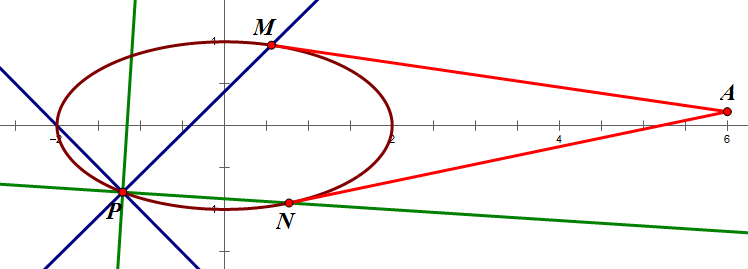
如上图，用同样的方法：
当 `B`, `C` 趋向 `M` 时，`l_2` 只能是 `PM` 或者垂直于 `PM` 于 `P`（蓝色的两线）；
当 `B`, `C` 趋向 `N` 时，`l_2` 只能是 `PN` 或者垂直于 `PN` 于 `P`（绿色的两线）。
那么，要满足题意，这两组垂线得重合，这样就得到了满足题意的一个必要条件：`PM\perp PN`！

于是作以 `MN` 为直径的圆，该圆与椭圆有两交点，记为 `P_1`, `P_2`，如下图：



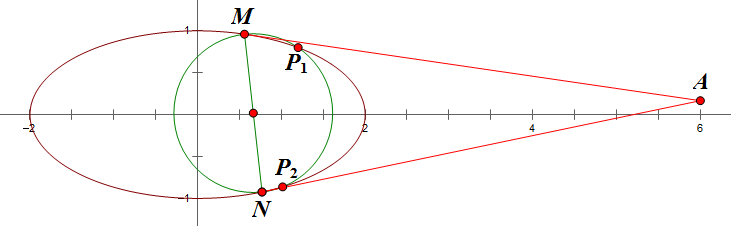
也就是说，`P` 只可能在 `P_1` 或 `P_2` 上。

如果在考场上的话，就别管充分性了，现在就可以计算那些点的坐标（如何计算简单貌似也是个问题）获得 `k_{P_1M}`, `k_{P_1N}`, `k_{P_2M}`, `k_{P_2N}` 后便可填写答案完事。

在这里的话，当然还得继续证明充分性。

经验告诉我这很有可能具有一般性，用软件画了下果然如此，于是赶紧写出以下的：

猜想：如下图，过椭圆外一定点 `A` 作两切线，切点分别为 `M`, `N`，以 `MN` 为直径作圆，若该圆与椭圆还有另外的交点 `P`，过 `A` 任作直线与椭圆交于 `B`, `C`，则 `PM` 和 `PN` 为 `\angle BPC` 的角平分线（一条内角一条外角）。



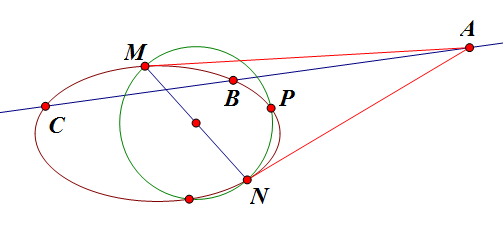
证明待续，先洗个鸟……

isee

回复 3# kuing

看到这个我想起来了，圆中的确有个平分的，但是一时找不到是回复那个了

===

搜调和搜到了，类似的，10楼，28楼 ，求证：三角形内切圆中的角相等

kuing

回复 4# isee

那……我上面那猜想怎么证明呢？我搞不定啊

kuing

定一下