向量数量积最值

12673zf

已知向量 $\vec{a} \cdot(\vec{a}+\vec{c})=0,|\vec{c}|=1,|\vec{a}+\vec{b}-2 \vec{c}|=2$ ，求 $\vec{a} \cdot \vec{b}$ 的最大值
分析了几何意义，没什么想法，请教大家

kuing

姑且认为是平面向量。



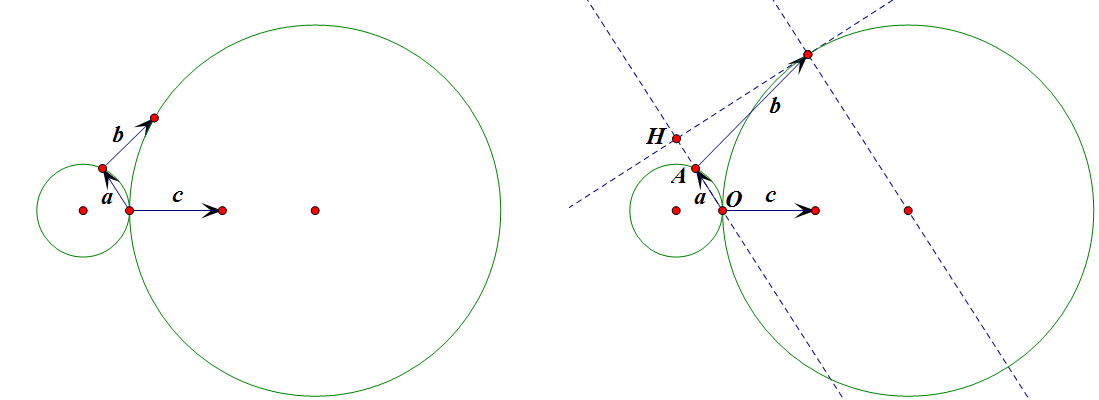
图形如上图（左），左边小圆半径为 `1/2`，右边大圆半径为 `2`。

当 `\bm a` 固定时，显然当 `\bm b` 为上图（右）的位置处 `\bm a\cdot\bm b` 取最大值，所以相当于求图中 `OA\cdot AH` 的最大值，设此时直线 `OA` 与 `\bm c` 所在直线的夹角为 `\theta`，则 `OA=\cos\theta`，易知 `OH=2-2\cos\theta`，则
\begin{align*}
OA\cdot AH&=\cos\theta\cdot(2-3\cos\theta)\\
&=\frac13\cdot3\cos\theta\cdot(2-3\cos\theta)\\
&\leqslant\frac13\left(\frac{3\cos\theta+2-3\cos\theta}2\right)^2\\
&=\frac13,
\end{align*}
当 `OA=1/3` 时取等，答案就是 `1/3`。